Ncert Exercises & Solutions

Given below in Column-I are the relations between vectors $a,$ $b,$ and $c$ and in Column-II are the orientations of $a,$ $b,$ and $c$ in the XY-plane. Match the relation in Column-I to the correct orientations in Column-II.

	Column-I		Column-II
a	$a + b = c$	(i)
b	$a- c = b$	(ii)
c	$b - a = c$	(iii)
d	$a + b + c = 0$	(iv)

1.	a(ii), b (iv), c(iii), d(i)
2.	a(i), b (iii), c(iv), d(ii)
3.	a(iv), b (iii), c(i), d(ii)
4.	a(iii), b (iv), c(i), d(ii)

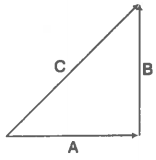
Hint: Apply triangle law of vector addition.

Step 1: Consider the adjacent diagram in which vectors A and B are corrected by head and tail.

Resultant vector C = A + B
(a) from (iv) it is clear that c = a + b
(b) from (iii) c + b = a $\Rightarrow$ a - c = b
(c) from (i) b = a +c $\Rightarrow$ b - a = c
(d) from (ii) - c = a + b $\Rightarrow$ a + b + c = 0

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions

	Column-I		Column-II
a	\(a + b = c\)	(i)
b	\(a- c = b\)	(ii)
c	\(b - a = c\)	(iii)
d	\(a + b + c = 0\)	(iv)