Consider the adjacent diagram.

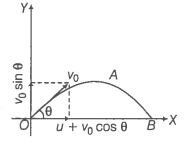
(a) Initial velocity in
$\begin{array}{l}\mathrm{x}\text{ -direction, }{\mathrm{u}}_{\mathrm{x}}= \mathrm{u} + {\mathrm{v}}_0\mathrm{cos\theta }\\ {\mathrm{u}}_{\mathrm{y}}=\text{ Initial velocity in }\mathrm{y}\text{ -direction }\\ = {\mathrm{v}}_0\mathrm{sin\theta }\end{array}$

where the angle of projection is $\mathrm{\theta }$.
Now, we can write

$\begin{array}{l}\tan \mathrm{\theta } = \frac{{\mathrm{u}}_{\mathrm{y}}}{{\mathrm{u}}_{\mathrm{x}}} = \frac{{\mathrm{u}}_0\sin \mathrm{\theta }}{\mathrm{u}+{\mathrm{u}}_0\cos \mathrm{\theta }}\\ \Rightarrow \mathrm{\theta } = {\tan }^{-1}\left(\frac{{\mathrm{v}}_0\sin \mathrm{\theta }}{\mathrm{u}+{\mathrm{v}}_0\cos \mathrm{\theta }}\right)\end{array}$

Step 2: Find the time of flight

(b) Let T be the time of flight.
As net vertical displacement is zero over the time period T
$\mathrm{y}=0, {\mathrm{u}}_{\mathrm{y}}={\mathrm{v}}_0\mathrm{sin\theta }, {\mathrm{a}}_{\mathrm{y}}=-\mathrm{g}, \mathrm{t}=\mathrm{T}$
We know that    $y\mathit{ }= u_{y}t\mathit{ }+ \frac{1}{2}{a}_y{t}^2$

$\begin{array}{l}\Rightarrow 0={\mathrm{v}}_0\sin \mathrm{\theta T}+\frac{1}{2}(-\mathrm{g}){\mathrm{T}}^2\\ \Rightarrow \mathrm{T}\left[{\mathrm{v}}_0\mathrm{sin\theta }-\frac{\mathrm{g}}{2}\mathrm{T}\right] = 0 \Rightarrow \mathrm{T}=0,\frac{2{\mathrm{v}}_0\sin \mathrm{\theta }}{\mathrm{g}}\\ \mathrm{T}=0\text{, corresponds to point }0\text{. }\\ \mathrm{Hence}, \mathrm{T}=\frac{2{\mathrm{u}}_0\sin \mathrm{\theta }}{\mathrm{g}}\end{array}$

Step 3: Find the horizontal range.

(c)

$\begin{array}{l}\text{ Horizontal range, }\mathrm{R} = (\mathrm{u}+{\mathrm{v}}_0\cos \mathrm{\theta })\mathrm{T}=(\mathrm{u}+{\mathrm{v}}_0\cos \mathrm{\theta })\frac{2{\mathrm{v}}_0\sin \mathrm{\theta }}{\mathrm{g}}\\ = \frac{{\mathrm{v}}_0}{\mathrm{g}}[2\mathrm{usin}\mathrm{\theta }+{\mathrm{v}}_0\sin 2\mathrm{\theta }]\end{array}$

Step 4: Apply maxima and minima and find the maximum horizontal ranges for different conditions.

(d)

$\text{ For horizontal range to be maximum, }\frac{dR}{d\theta }=0$

$\begin{array}{l}\Rightarrow \frac{{\mathrm{v}}_0}{\mathrm{g}}[2\mathrm{ucos}\mathrm{\theta }+{\mathrm{v}}_0\cos 2\mathrm{\theta }\times 2]=0\\ \Rightarrow 2\mathrm{ucos}\mathrm{\theta }+2{\mathrm{v}}_0[2{\cos }^2\mathrm{\theta }-1]=0\\ \Rightarrow 4{\mathrm{v}}_0{\cos }^2\mathrm{\theta }+2\mathrm{ucos}\mathrm{\theta }-2{\mathrm{v}}_0=0\\ \Rightarrow 2{\mathrm{v}}_0{\cos }^2\mathrm{\theta }+\mathrm{ucos}\mathrm{\theta }-{\mathrm{v}}_0=0\\ \Rightarrow \cos \mathrm{\theta }=\frac{-\mathrm{u}\pm \sqrt{{\mathrm{u}}^2+8{\mathrm{v}}_0^2}}{4{\mathrm{v}}_0}\\ \Rightarrow {\mathrm{\theta }}_{\max }={\cos }^{-1}\left[\frac{-\mathrm{u}\pm \sqrt{{\mathrm{u}}^2+8{\mathrm{v}}_0^2}}{4{\mathrm{v}}_0}\right]\\ ={\cos }^{-1}\left[\frac{-\mathrm{u}+\sqrt{{\mathrm{u}}^2+8{\mathrm{v}}_0^2}}{4{\mathrm{v}}_0}\right]\end{array}$

(e) If $\mathrm{u} = {\mathrm{v}}_0$

$\cos \mathrm{\theta }=\frac{-{\mathrm{v}}_0\pm \sqrt{{\mathrm{v}}_0^2+8{\mathrm{v}}_0^2}}{4{\mathrm{v}}_0}=\frac{-1+3}{4}=\frac{1}{2}$
$\Rightarrow \mathrm{\theta }={60}^{\circ }$
$\begin{array}{l}\text{ If }\mathrm{u}<<{\mathrm{v}}_0,\text{ then }8{\mathrm{v}}_0^2+{\mathrm{u}}^2\approx 8{\mathrm{v}}_0^2\\ \begin{array}{c}{\mathrm{\theta }}_{\max }={\cos }^{-1}\left[\frac{-\mathrm{u}\pm 2\sqrt{2}{\mathrm{v}}_0}{4{\mathrm{v}}_0}\right]={\cos }^{-1}\left[\frac{1}{\sqrt{2}}-\frac{\mathrm{u}}{4{\mathrm{v}}_0}\right]\\ {\mathrm{\theta }}_{\max } = {\cos }^{-1}\left[\frac{1}{\sqrt{2}}\right] = \frac{\mathrm{\pi }}{4}\\ \mathrm{u}>>{\mathrm{v}}_0\\ {\mathrm{\theta }}_{\max }={\cos }^{-1}\left[\frac{-\mathrm{u}\pm \mathrm{u}}{4{\mathrm{v}}_0}\right] = 0 \Rightarrow {\mathrm{\theta }}_{\max } = \frac{\mathrm{\pi }}{2}\end{array}\end{array}$

(f) If $\mathrm{u} = 0, {\mathrm{\theta }}_{\max } = {\cos }^{-1}\left[\frac{0\pm \sqrt{8{\mathrm{v}}^{2}0}}{4{\mathrm{v}}_0}\right] = {\cos }^{-1}\left(\frac{1}{\sqrt{2}}\right) = {45}^{\circ }$