Ncert Exercises & Solutions

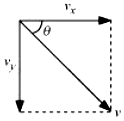
Question 5.11:

A truck starts from rest and accelerates uniformly at 2.0 m s ^-2. At t = 10 s, a stone is dropped by a person standing on the top of the truck (6 m high from the ground). What are
(a) velocity, and
(b) acceleration of the stone at t = 11 s? (Neglect air resistance.)

Initial velocity, u = 0, a =0, t = 10 s

Let v be the velocity of the truck when the stone is dropped from it after t = 10 s.
Using the relation, v = u + at, we get
υ = 0 + 2.0 x 10 = 20 m/s(a) Horizontal velocity of the stone when it is dropped from the truck is
υ_x = v = 20 m/s
As air resistance is neglected, so υ_x = constant.
Motion in the vertical direction :
Initial velocity of the stone, υ_y = 0 at t = 10 s
acceleration, a_y = g = 10 m s^-2, time t = 11-10 = 1 s
If v_y be velocity of the stone after 1 s of drop (i.e. at t = 11 s,) then

v_{y}

u_{y}

+ a_yt = 0 + 10 x 1 = 10 m s^-1If v be the velocity of the stone after 11s, then

v = \sqrt{{v_{x}}^{2} + {v_{y}}^{2}}

= \sqrt{{(20)}^{2} + {(10)}^{2}}

= \sqrt{500} = 22.4 m s^{- 1}

L e t θ b e t h e a n g l e w h i c h r e s u l \tan t v e l o c i t y m a k e s t h e h o r i z o n t a l d i r e c t i o n

T h e n \tan θ = \frac{v_{y}}{v_{x}} = \frac{10}{20} = 0.5

\Rightarrow θ = 26 . 6^{0}

(b) At the moment, the stone is dropped from the truck, the horizontal force on the stone is zero,so,
a_x = 0 and a_y = acceleration along vertical direction = +g = 10 m s^-2 which acts in downward direction.
If a = resultant acceleration of the stone, then

a = \sqrt{{a_{x}}^{2} + {a_{y}}^{2}} = \sqrt{0^{2} + {(10)}^{2}}

\Rightarrow a = 10 m s^{- 2} (V e r t i c a l l y d o w n w a r d)

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions