The given system of two masses and a pulley can be represented as shown in the following figure:

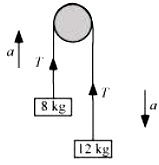
Smaller mass, $m_1$ = 8 kg

Larger mass, $m_2$= 12 kg

Tension in the string = T

Mass $m_2$, owing to its weight, moves downward with acceleration a, and mass $m_1$ moves upward.

Applying Newton’s second law of motion to the system of each mass:

For mass$m_1$  : The equation of motion can be written as:

T – $m_1$g = ma     …………… (i)

For mass $m_2$: The equation of motion can be written as:

$m_{2}g-T=m_{2}a ...........\left(ii\right)$

Adding equations (i) and (ii), we get:

$\left({\mathrm{m}}_2 - {\mathrm{m}}_1\right)\mathrm{g} = \left({\mathrm{m}}_1 + {\mathrm{m}}_2\right)\mathrm{a}$
$\Rightarrow \mathrm{a} = \left(\frac{{\mathrm{m}}_2 = {\mathrm{m}}_1}{{\mathrm{m}}_1 +\hspace{0.17em}{\mathrm{m}}_2}\right)\mathrm{g}$
$= \left(\frac{12 - 8}{12 + 8}\right) \times 10 = 2 \mathrm{m}/{\mathrm{s}}^2$

Therefore, the acceleration of the masses is 2 m/s2.

Substituting the value of a in equation (ii), we get:

${\mathrm{m}}_2\mathrm{g} - \mathrm{T} = {\mathrm{m}}_2\left(\frac{{\mathrm{m}}_2 - {\mathrm{m}}_1}{{\mathrm{m}}_1 + {\mathrm{m}}_2}\right)\mathrm{g}$
$\mathrm{T} = \left({\mathrm{m}}_2 - \frac{{\mathrm{m}}_2^2 - {\mathrm{m}}_1{\mathrm{m}}_2}{{\mathrm{m}}_1 + {\mathrm{m}}_2}\right)g$
$= \left(\frac{2{\mathrm{m}}_1{\mathrm{m}}_2}{{\mathrm{m}}_1 + {\mathrm{m}}_2}\right)\mathrm{g}$
$= \left(\frac{2 \times 12 \times 8}{12 + 8}\right) \times 10$
$= \frac{2 \times 12 \times 8}{20} \times 10 = 96 \mathrm{N}$

Therefore, the tension in the string is 96 N.