Question 7. 21. A solid cylinder rolls up an inclined plane of angle of inclination 30°. At the bottom of the inclined plane, the centre of mass of the cylinder has a speed of 5 m/s.
(a) How far will the cylinder go up the plane?
(b) How long will it take to return to the bottom?
Velocity of the solid cylinder, v = 5 m/s
Angle of inclination, θ = 30°
Height reached by the cylinder =h
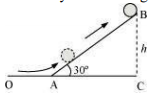
Energy of the cylinder at point A:
Energy of the cylinder at point B = mgh
Using the law of conservation of energy,
In ΔABC:
Hence, the cylinder will go 3.82 m up the inclined plane.
(b) For a radius of gyration K, the velocity of the cylinder at the instance when it rolls back to the bottom is,
The time taken to return to the bottom is,
Therefore, the total time taken by the cylinder to return to the bottom

© 2025 GoodEd Technologies Pvt. Ltd.