Ncert Exercises & Solutions

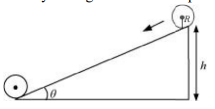
Question 7. 27. Prove the result that the velocity v of translation of a rolling body (like a ring, disc, cylinder, or sphere) at the bottom of an inclined plane of a height h is given by,v²=2gh/(1+k²/R²) using dynamical consideration (i.e., by consideration of forces and torques). Note k is the radius of gyration of the body about its symmetry axis, and R is the radius of the body. The body starts from rest at the top of the plane.

A body rolling on an inclined plane of height h, is shown in the following figure:

m = Mass of the body
R = Radius of the body
K = Radius of gyration of the body
v = Translational velocity of the
body h =Height of the inclined
plane g = Acceleration due to
gravity
Total energy at the top of the plane, E1= mgh
Total energy at the bottom of the plane,

E_{b} = K E_{r v} + K E_{trans}

\begin{array}{l} = \frac{1}{2} {Iω}^{2} + \frac{1}{2} {mv}^{2} \\ But I = {mk}^{2} and ω = \frac{v}{R} \end{array}

\begin{array}{l} ∴ E_{b} = \frac{1}{2} ({mk}^{2}) (\frac{v^{2}}{R^{2}}) + \frac{1}{2} {mv}^{2} \\ = \frac{1}{2} {mv}^{2} \frac{k^{2}}{R^{2}} + \frac{1}{2} {mv}^{2} \\ = \frac{1}{2} {mv}^{2} (1 + \frac{k^{2}}{R^{2}}) \end{array}

From the law of conservation of energy, we have:

\begin{array}{l} E_{T} = E_{b} \\ mgh = \frac{1}{2} {mv}^{2} (1 + \frac{k^{2}}{R^{2}}) \\ ∴ v = \frac{2 gh}{(1 + k^{2} / R^{2})} \end{array}

Hence, the given result is proved.

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions