Ncert Exercises & Solutions

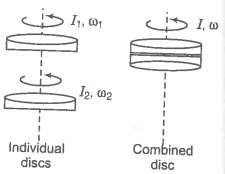
Q. 24 Two discs of moments of inertia $I_{1} and I_{2}$ about their respective axes (normal to the disc and passing through the center), and rotating with angular speed $ω_{1}$ and $ω_{2}$ are brought into contact face to face with their axes of rotation coincident.

(a) Does the law of conservation of angular momentum apply to the situation? Why?

(b) Find the angular speed of the two discs system.

(d) Account for this loss.

Hint: If external torque is zero then angular momentum is conserved.

Step 1: Interpret about net external torque.

Consider the diagram below Let the common angular velocity of the system is

ω

(a) Yes, the law of conservation of angular moment can be applied. Because there is no net external torque on the system of the two discs. External forces, gravitation, and normal reaction act through the axis Of rotation, hence, produce no torque.

Step 2: Find the angular speed of the two discs system by applying angular momentum conservation.

(b) By conservation of angular momentum

\begin{array}{l} L_{f} = L_{i} \\ \Rightarrow Iω = I_{1} ω_{1} + I_{2} ω_{2} \\ \Rightarrow ω = \frac{I_{1} ω_{1} + I_{2} ω_{2}}{I} = \frac{I_{1} ω_{1} + I_{2} ω_{2}}{I_{1} + I_{2}} (∵ I = I_{1} + I_{2}) \end{array}

Step 3: Find the loss in kinetic energy.

(c)

\begin{array}{l} K_{t} = \frac{1}{2} (I_{1} + I_{2}) \frac{(I_{1} ω_{1} + I_{2} ω_{2})^{2}}{(I_{1} + I_{2})^{2}} = \frac{1}{2} \frac{(I_{1} ω_{1} + I_{2} ω_{2})^{2}}{(I_{1} + I_{2})} \\ K_{i} = \frac{1}{2} (I_{1} ω_{1}^{2} + I_{2} ω_{2}^{2}) \\ ΔK = K_{f} - K_{i} = - \frac{I_{1} I_{2}}{2 (I_{1} + I_{2})} (ω_{1} - ω_{2})^{2} < 0 \end{array}

Step 4: Account for the above loss

(d) Hence, there is a loss in KE of the system, The loss in kinetic energy is mainly due to the work against the friction between the two discs.

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions