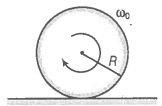
Q. 25 A disc of radius R is rotating with an angular about a horizontal axis. It is placed on a horizontal table. The coefficient of kinetic friction is .
(a) What was the velocity of its center of mass before being brought in contact with the table?
(b) What happens to the linear velocity of a point on its rim when placed in contact with the table?
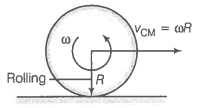
(c) What happens to the linear speed of the center of mass when the disc is placed in contact with the table?
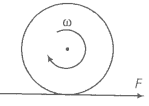
(d) Which force is responsible for the effects in (b) and (c)?
(e) What condition should be satisfied with rolling to begin?
(f) Calculate the time taken for the rolling to begin.

© 2025 GoodEd Technologies Pvt. Ltd.