Ncert Exercises & Solutions

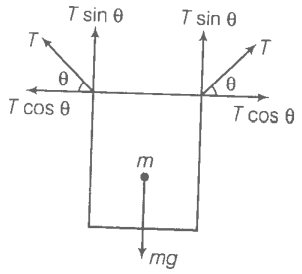
A rectangular frame is to be suspended symmetrically by two strings of equal length on two supports (figure). It can be done in one of the following three ways;

The tension in the strings will be:

1.	the same in all cases.	2.	least in (a).
3.	least in (b).	4.	least in (c).

(3) Hint: The weight of the frame is balanced by the tension developed in the strings.

Step 1: Find the tension developed in the strings in a general case.

Consider the FBD diagram of the rectangular frame.

Balancing vertical forces,

2 T sinθ - mg = 0

[T is the tension in the strings]

\Rightarrow

2 T sinθ = mg

...(i)

Total horizontal force =

T cosθ - T cosθ = 0

Now from Eq. (i),

T = \frac{mg}{2 sinθ}

Step 2: Find the minimum tension in the strings.

As mg is constant,

T \propto \frac{1}{sinθ}

T_{\min} = \frac{mg}{2 {sinθ}_{\max}}

(since,

{sinθ}_{\max} = 1

)

{sinθ}_{\max} = 1 \Rightarrow θ = 90 °

Matches with option(b).

Hence, the tension is least for case(b).

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions