Ncert Exercises & Solutions

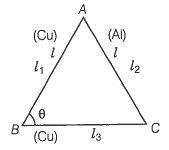
Q.27. An equilateral triangle ABC is formed by two Cu rods AB and BC and one Al rod. It is heated in such a way that the temperature of each rod increases by $Δ T$ $Δ T$ . Find the change in the angle ABC. [coeffecient of linear expansion for Cu is $α_{1}$ $α_{1}$ , coefficient of linear expansion for Al is $α_{2}$ $α_{2}$ ]

Hint: The change in temperature produces strain in the rods.

Step 1: Find a relation between the lengths of the rods and the angle of the triangle.

Consider the diagram shown.

Let

l_{1} = A B, l_{2} = A C, l_{3} = B C

$l_{1} = A B, l_{2} = A C, l_{3} = B C$

∴

$∴$

cos θ = \frac{l_{3}^{2} + l_{1}^{2} - l_{2}^{2}}{2 l_{3} l_{1}}

$\cos θ = \frac{l_{3}^{2} + l_{1}^{2} - l_{2}^{2}}{2 l_{3} l_{1}}$ (assume

∠ A B C = θ

$∠ A B C = θ$ )

\Rightarrow 2 l_{3} l_{1} cos θ = l_{3}^{2} + l_{1}^{2} - l_{2}^{2}

$\Rightarrow 2 l_{3} l_{1} \cos θ = l_{3}^{2} + l_{1}^{2} - l_{2}^{2}$

Step 2: Differentiate on both sides.

Differentiating,

2 (l_{3} d l_{1} + l_{1} d l_{3}) cos θ - 2 l_{1} l_{3} sin θ d θ

$2 (l_{3} d l_{1} + l_{1} d l_{3}) \cos θ - 2 l_{1} l_{3} \sin θ d θ$

= 2 l_{3} d l_{1} + 2 l_{1} d l_{1} - 2 l_{2} d l_{2}

$= 2 l_{3} d l_{1} + 2 l_{1} d l_{1} - 2 l_{2} d l_{2}$
Now,

d l_{1} = l_{1} α_{1} Δ t

$d l_{1} = l_{1} α_{1} Δ t$ (where

Δ

$Δ$ t = change in temperature)
and

l_{1} = l_{2} = l_{3} = l

$l_{1} = l_{2} = l_{3} = l$

(l^{2} α_{1} Δ t + l^{2} α_{1} Δ t) cos θ + l^{2} sin θ d θ = l^{2} α_{1} Δ t + l^{2} α_{1} Δ t - l^{2} α_{2} Δ t

$(l^{2} α_{1} Δ t + l^{2} α_{1} Δ t) \cos θ + l^{2} \sin θ d θ = l^{2} α_{1} Δ t + l^{2} α_{1} Δ t - l^{2} α_{2} Δ t$

$\sin θ d θ = 2 α_{1} Δ t (1 - \cos θ) - α_{2} Δ t$
Putting,

$θ = 60 °$ (for equilateral triangle)

$d θ \times \sin 60 ° = 2 α_{1} Δ t (1 - \cos 60 °) - α_{2} Δ t$

$= 2 α_{1} Δ t \times \frac{1}{2} - α_{2} Δ t = (α_{1} - α_{2}) Δ t$

Step 3: Find the change in angle.

$\Rightarrow$

$d θ =$ change in the angle

$∠ A B C$

$= \frac{(α_{1} - α_{2}) Δ T}{\sin 60 °} = \frac{2 (α_{1} - α_{2}) Δ T}{\sqrt{3}} (∵ Δ t = Δ T g i v e n)$

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions