Ncert Exercises & Solutions

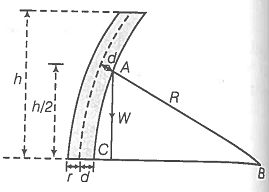
Q.28. In nature, the failure of structural members usually results from large torque because of twisting or bending rather than due to tensile or compressive strains. This process of structural breakdown is called buckling and in cases of tall cylindrical structures like trees, the torque is caused by its own weight bending the structure. Thus, the vertical through the centre of gravity does not fall within the base. The elastic torque caused because of this bending about the central axis of the tree is given by $\frac{Y π r^{4}}{4 R} .$ Y is Young's modulus, r is the radius of the trunk and R is the radius of curvature of the bent surface along the height of the tree containing the centre of gravity (the neutral surface). Estimate the critical height of a tree for a given radius of the trunk.

Hint: The critical height of the tree depends on the maximum torque it can survive.

Step 1: Find the torque about the base of the tree.

Consider the diagram according to the question, the bending torque on the trunk of the radius r of the tree is

\frac{Y π r^{4}}{4 R} .

where R is the radius of curvature of the bent surface. When the tree is about to buckle,

Torque=Wxd =

\frac{Y π r^{4}}{4 R} .

Step 2: Find the value of d.

R ≫ h_{1}

, then the centre of gravity is at a height

l \approx \frac{1}{2} h

from the ground.

From

Δ A B C, R^{2} \approx (R - d)^{2} + {(\frac{1}{2} h)}^{2}

d ≪ R, R^{2} \approx R^{2} - 2 R d + \frac{1}{4} h^{2}

∴

d = \frac{h^{2}}{8 R}

Step 3: Find the value of critical height.

W_{0}

is the weight/volume,

\frac{Y π r^{4}}{4 R} = W_{0} (π r^{2} h) \frac{h^{2}}{8 R} [∵ Torque is caused by the weight]

\Rightarrow

h = {(\frac{2 Y}{W_{0}})}^{1 / 3} r^{2 / 3}

Hence, the critical height

= h = {(\frac{2 Y}{W_{0}})}^{1 / 3} r^{2 / 3}

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions