Ncert Exercises & Solutions

Q. 18 Two mercury droplets of radii 0.1 cm and 0.2 cm collapse into one single drop. What amount of energy is released? The surface tension of mercury is $T = 435.5 \times 10^{- 3} N m^{- 1} .$ $T = 435.5 \times 10^{- 3} N m^{- 1} .$

Hint: The energy released will be equal to the change in surface energy.

Step 1: Find the change in surface area.

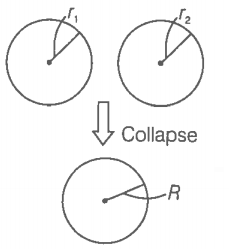
Consider the diagram.

Radii of mercury droplets,

r_{1} = 0.1 c m = 1 \times 10^{- 3} m

$r_{1} = 0.1 c m = 1 \times 10^{- 3} m$

r_{2} = 0.2 c m = 2 \times 10^{- 3} m

$r_{2} = 0.2 c m = 2 \times 10^{- 3} m$

Surface tension, (T) = 435.5 x

10^{- 3}

$10^{- 3}$ N/m

Let the radius of the big drop formed by collapsing be R.

∴

$∴$ The volume of big drop=Volume of small droplets

\frac{4}{3} {πR}^{3} = \frac{4}{3} {πr}_{1}^{3} + \frac{4}{3} {πr}_{2}^{2}

$\frac{4}{3} {πR}^{3} = \frac{4}{3} {πr}_{1}^{3} + \frac{4}{3} {πr}_{2}^{2}$

R^{3} = r_{1}^{3} + r_{2}^{3}

$R^{3} = r_{1}^{3} + r_{2}^{3}$

= {(0.1)}^{3} + {(0.2)}^{3} = 0.001 + 0.008

$= {(0.1)}^{3} + {(0.2)}^{3} = 0.001 + 0.008$

= 0.009

$= 0.009$

or R =

0.21 c m = 2.1 \times 10^{- 3} m

$0.21 c m = 2.1 \times 10^{- 3} m$

∴

$∴$ Change in surface area,

Δ A = 4 {πR}^{2} - (4 {πr}_{1}^{2} + 4 {πr}_{2}^{2})

$∆ A = 4 {πR}^{2} - (4 {πr}_{1}^{2} + 4 {πr}_{2}^{2})$

= 4 π [R^{2} - (r_{1}^{2} + r_{2}^{2})]

$= 4 π [R^{2} - (r_{1}^{2} + r_{2}^{2})]$

Step 2: Find the change in surface energy.

∴

$∴$ The energy released

= T . Δ A

$= T . ∆ A$ (where T is the surface tension of mercury)

$= 435.5 \times 10^{- 3} \times 4 \times 3.14 \times [{(2.1 \times 10^{- 3})}^{2} - {(1 \times 10^{- 3})}^{2} - {(2 \times 10^{- 3})}^{2}] = - 3.22 \times 10^{- 6} J$

(The negative sign shows absorption)

Therefore, 3.22

$\times 10^{- 6}$ J energy will be absorbed.

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions