Ncert Exercises & Solutions

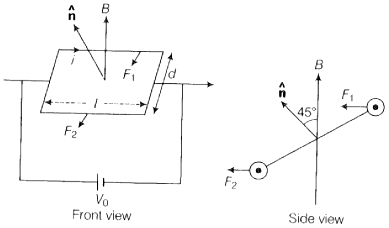
A rectangular conducting loop consists of two wires on two opposite sides of length l joined together by rods of length d. The wires are each of the same material but with cross-sections differing by a factor of 2. The thicker wire has a resistance R and the rods are of low resistance, which in turn are connected to a constant voltage source $V_{0}$ . The loop is placed in uniform a magnetic field B at 45° to its plane. Find $τ$ , the torque exerted by the magnetic field on the loop about an axis through the centers of rods.

Hint: The presence of a magnetic field results in torque on the loop.

The thicker wire has a resistance R, then the other wire has a resistance 2R as the wires are of the same material but with cross-sections differing by a factor of 2.

Step 1: Now, the force and hence, torque on the first wire is given by;

F_{1} = i_{1} lB = \frac{V_{0}}{R} lB, τ_{1} = \frac{d}{2 \sqrt{2}} F_{1} = \frac{V_{0} ldB}{2 \sqrt{2} R}

Step 2: Similarly, the force, hence, torque on other wire is given by;

\begin{array}{l} F_{2} = i_{2} lB = \frac{V_{0}}{2 R} IB, τ_{2} = \frac{d}{2 \sqrt{2}} F_{2} = \frac{V_{0} ldB}{4 \sqrt{2} R} \\ So, net torque, τ = τ_{1} - τ_{2} \\ τ = \frac{1}{4 \sqrt{2}} \frac{V_{0} ldB}{R} \end{array}

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions