Ncert Exercises & Solutions

Verify Ampere's law for the magnetic field of a point dipole of dipole moment m = m $\hat{k}$ . Take C as the closed curve running clockwise along:

(i) the z-axis from z = a > 0 to z = R,
(ii) along the quarter circle of radius R and center at the origin in the first quadrant of xz-plane,
(iii) along the x-axis from x = R to x = a, and
(iv) along the quarter circle of radius a and center at the origin in the first quadrant of xz-plane

Hint: Use the formula of the magnetic field due to a bar magnet.

From P to Q, every point on the z-axis lies at the axial line of magnetic dipole of moment M. Magnetic field induction at a point at distance z from the magnetic dipole of moment M is:

| B | = \frac{μ_{0}}{4 π} \frac{2 | M |}{z^{3}} = \frac{μ_{0} M}{2 {πz}^{3}}

Step 1:

(i) Along z-axis from P to Q:

\int_{P}^{Q} B . dl = \int_{P}^{Q} B . dl \cos 0 ° = \int_{a}^{R} B dz

\begin{array}{l} = \int_{a}^{R} \frac{μ_{0}}{2 π} \frac{M}{z^{3}} dz = \frac{μ_{0} M}{2 π} (\frac{- 1}{2}) (\frac{1}{R^{2}} - \frac{1}{a^{2}}) \\ = \frac{μ_{0} M}{4 π} (\frac{1}{a^{2}} - \frac{1}{R^{2}}) \end{array}

Step 2:

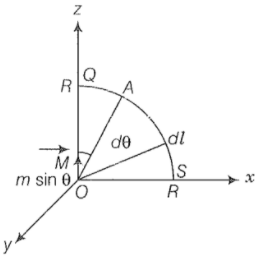
(ii) Along the quarter circle QS of radius R is given in the figure below,

The point A lies on the equatorial line of the magnetic dipole of moment Msin

θ

. The Magnetic field at point A on the circular arc is:

B = \frac{μ_{0}}{4 π} \frac{Msi θ}{R^{3}}; dl = Rdθ

∴ \int B \cdot dI = \int B \cdot dlcos θ = \int_{0}^{\frac{π}{2}} \frac{μ_{0}}{4 π} \frac{Msin θ}{R^{3}} Rdθ

= \frac{μ_{0}}{4 π} \frac{M}{R^{2}} (- \cos θ)_{0}^{π / 2} = \frac{μ_{0}}{4 π} \frac{M}{R^{2}}

Step 3:

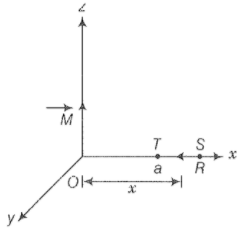
(iii) Along the x-axis over the path ST, consider the figure given ahead;

From the figure, every point lies on the equatorial line of the magnetic dipole. Magnetic field induction at a point at distance x from the dipole is,

B = \frac{μ_{0}}{4 π} \frac{M}{x^{3}}

∴ \int_{S}^{T} B \cdot dl = \int_{R}^{a} - \frac{μ_{0} M}{4 {πx}^{3}} \cdot dl = 0 [∵ angle between (- M) and dl is 90 °]

Step 4:

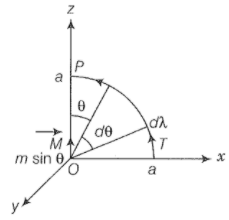
(iv) Along with the quarter circle TP of radius a. Consider the figure given below.

From case (i), we get line integral of B along the quarter circle TP of radius a;

\int B \cdot dl = \int_{π / 2}^{0} \frac{μ_{0}}{4 π} \frac{Msin θ}{a^{3}} adθ

\begin{array}{l} = \frac{μ_{0}}{4 π} \frac{M}{a^{2}} \int_{π / 2}^{0} \sin θdθ = \frac{μ_{0}}{4 π} \frac{M}{a^{2}} [- \cos θ]_{π / 2}^{0} \\ = \frac{- μ_{0}}{4 π} \frac{M}{a^{2}} \end{array}

∴ \oint_{PQST} B \cdot dl = \int_{P}^{Q} B \cdot dl + \int_{Q}^{S} B \cdot dl + \int_{S}^{T} B \cdot dl + \int_{T}^{P} B \cdot dl

= \frac{μ_{0} M}{4 π} [\frac{1}{a^{2}} - \frac{1}{R^{2}}] + \frac{μ_{0}}{4 π} \frac{M}{R^{2}} + 0 + (- \frac{μ_{0}}{4 π} \frac{M}{a^{2}}) = 0

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions