Ncert Exercises & Solutions

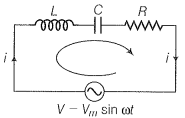
For an L-C-R circuit driven at a frequency $ω$ $ω$ , the equation reads

$L \frac{d i}{d t} + R i + \frac{q}{C} = V_{i} = V_{m} sin ω t$ $L \frac{d i}{d t} + R i + \frac{q}{C} = V_{i} = V_{m} \sin ω t$

a.	Multiply the equation by i and simplify where possible.
b.	Interpret each term physically.
c.	Cast the equation in the form of conservation of energy statement.
d.	Integrate the equation over the one cycle to find that the phase difference between V and i must be acute.

Hindi: Use Kirchoff's law.

Step 1: Consider the L-C-R circuit. Applying KVL for the loop, we can write;

\Rightarrow L \frac{d i}{d t} + \frac{q}{C} + i R = V_{m} sin ω t . . . (i)

$\Rightarrow L \frac{d i}{d t} + \frac{q}{C} + i R = V_{m} \sin ω t . . . (i)$

Step 2: Multiplying both sides by i, we get;

L i \frac{d t}{d t} + \frac{q}{C} i + i^{2} R = (V_{m} i) sin ω t = V i . . . (i i)

$L i \frac{d t}{d t} + \frac{q}{C} i + i^{2} R = (V_{m} i) \sin ω t = V i . . . (i i)$

w h e r e L i \frac{d i}{d t} = \frac{d}{d t} (\frac{1}{2} L i^{2})

$w h e r e L i \frac{d i}{d t} = \frac{d}{d t} (\frac{1}{2} L i^{2})$ =rate of change of energy stored in the inductor.

R i^{2}

$R i^{2}$ =joule heating loss

\frac{q}{C} i = \frac{d}{d t} (\frac{q^{2}}{2 C}) =

$\frac{q}{C} i = \frac{d}{d t} (\frac{q^{2}}{2 C}) =$ rate of change of energy stored in the capacitor.

Vi=rate at which driving force pours in energy. It goes into (i) ohmic loss and (ii) increase of stored energy.

Hence Eq. (ii) is in the form of conservation of energy statements.

Step 3: Integrating both sides of Eq. (ii) with respect to time over one full cycle

(0 \to T)

$(0 \to T)$ , we may write;

\int_{0}^{T} \frac{d}{d t} (\frac{1}{2} L i^{2} + \frac{q^{2}}{2 C}) d t + \int_{0}^{T} R i^{2} d t = V i d t

$\int_{0}^{T} \frac{d}{d t} (\frac{1}{2} L i^{2} + \frac{q^{2}}{2 C}) d t + \int_{0}^{T} R i^{2} d t = V i d t$

\Rightarrow 0 + (+ v e) = \int_{0}^{T} V i d t

$\Rightarrow 0 + (+ v e) = \int_{0}^{T} V i d t$

\Rightarrow \int_{0}^{T} Vi dt > 0

$\Rightarrow \int_{0}^{T} Vi dt > 0$ if the phase difference between V and i is a constant and acute angle.