Hint: Use Kirchoff's law.
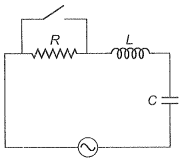
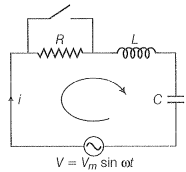
Step 1: (a) Consider the R-L-C circuit shown in the adjacent diagram.
Given,
Let current at any instant be i.
Applying KVL in the given circuit;
Now, we can write,
From Eq. (i),
This is the required equation of variation (motion) of charge.
(b) Step 2:
Step 3: When R is short-circuited at , the energy is stored in L and C.
(c) Step 4: When R is short-circuited, the circuit becomes an L-C oscillator. The capacitor will go on discharging and all energy will go to L and back and forth. Hene, there is an oscillation of energy from electrostatic to magnetic and magnetic to electrostatic.