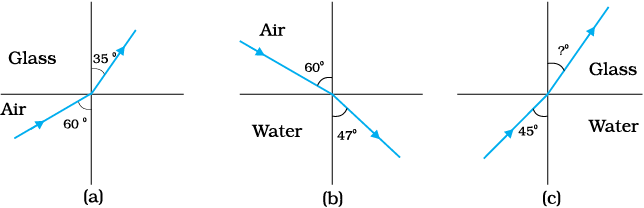
9.4 Figures 9.31(a) and (b) show the refraction of a ray in air incident at 60° with the normal to a glass-air and water-air interface, respectively. Predict the angle of refraction in the glass when the angle of incidence in water is 45° with the normal to a water-glass interface [Fig. 9.31(c)].
Hint: Apply snell's law
Step 1: Find the refractive index of glass.
For the glass-air interface:
Angle of incidence, i =60°
Angle of refraction, r=35°
The relative refractive index of the glass with respect to air,
Step 2: Find the refractive index of water.
For the air-water interface:
The angle of incidence, i=60°
The angle of refraction, r=47°
The relative refractive index of the water with respect to air,
Step 3: Find the refractive index of glass with respect to water.
The relative refractive index of glass with respect to water:

Step 4: Find the angle of refraction at the water-glass interface.
For the glass-water interface:
The angle of incidence, i= 45°
Let the angle of refraction = r
From Snell’s law,
Hence, the angle of refraction at the water-glass interface is 38.68°.

© 2025 GoodEd Technologies Pvt. Ltd.