Hint: The refraction of light depends on the refractive index of the material.

Step 1: Find the angle of refraction at the first surface.

Any ray entering at an angle i shall be guided along AC if the angle ray makes with a face AC $\left(\mathrm{\varphi }\right)$ is greater than the critical angle as per the principle of total internal reflection.

So, $\mathrm{\varphi }+\mathrm{r}=90°$, therefore, sin $\mathrm{\varphi }$ = cos r

                                               
$\Rightarrow \sin \mathrm{\varphi }\ge \frac{1}{\mathrm{\mu }}$
$\Rightarrow \cos \mathrm{r}\ge \frac{1}{\mathrm{\mu }}$
$\mathrm{or} 1-{\cos }^2\mathrm{r}\le 1-\frac{1}{{\mathrm{\mu }}^2}$
$\mathrm{i}.\mathrm{e}., {\sin }^2\mathrm{r}\le 1-\frac{1}{{\mathrm{\mu }}^2}$
$\mathbf{Step}\mathbf{ }\mathbf{2}\mathbf{:} \mathrm{Find} \mathrm{the} \mathrm{angle} \mathrm{of} \mathrm{incidence}.$
$\mathrm{Since}, \sin \mathrm{i}= \mathrm{\mu } \mathrm{sinr}$
$\frac{1}{{\mathrm{\mu }}^2}{\sin }^2 \mathrm{i}\le 1-\frac{1}{{\mathrm{\mu }}^2} \mathrm{or} {\sin }^2 \mathrm{i}\le {\mathrm{\mu }}^2-1$
$\mathrm{When} \mathrm{i}=\frac{\mathrm{\pi }}{2}, \mathrm{we} \mathrm{have} \mathrm{the} \mathrm{smallest} \mathrm{angle} \mathrm{\varphi }.$

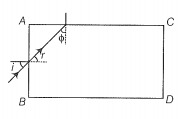
Step 3: Find the refractive index of the material.
If that is greater than the critical angle, then all other angles of incidence shall be more than the critical angle.
Thus,                                 $1\le {\mathrm{\mu }}^2-1$
or                                       ${\mathrm{\mu }}^2\ge 2$
$\Rightarrow \mathrm{\mu }\ge \sqrt{2}$
This is the required result.