Ncert Exercises & Solutions

Consider a ray of light incident from the air onto a slab of glass (refractive index $n$) of width $d$, at an angle $\theta$. The phase difference between the ray reflected by the top surface of the glass and the bottom surface is:
1. $\frac{4 \pi d}{\lambda}\left(1-\frac{1}{n^2} \sin ^2 \theta\right)^{1 / 2}+\pi$
2. $\frac{4 \pi d}{\lambda}\left(1-\frac{1}{n^2} \sin ^2 \theta\right)^{1 / 2}$
3. $\frac{4 \pi d}{\lambda}\left(1-\frac{1}{n^2} \sin ^2 \theta\right)^{1 / 2}+\frac{\pi}{2}$
4. $\frac{4 \pi d}{\lambda}\left(1-\frac{1}{n^2} \sin ^2 \theta\right)^{1 / 2}+2\pi$

(a) Hint: The ray reflected by the bottom surface covers an extra path inside the slab.

Step 1: Find the time taken by the ray to move into the slab.

Consider the diagram, the ray (P) is incident at an angle $θ$ and gets reflected in the direction P' and refracted in the direction P". Due to reflection from the glass medium, there is a phase change of $π$ .

Time taken to travel along OP''

$∆ t = \frac{OP''}{v} = \frac{d / cosr}{c / n} = \frac{nd}{ccosr}$

From Snell's law,

$n = \frac{sinθ}{sinr}$
$\Rightarrow sinr = \frac{sinθ}{n}$
$cosr = \sqrt{1 - \sin^{2} r} = \sqrt{1 - \frac{\sin^{2} θ}{n^{2}}}$

$∆ t = \frac{nd}{c {(1 - \frac{\sin^{2} θ}{n^{2}})}^{1 / 2}} = \frac{nd}{c} {(1 - \frac{\sin^{2} θ}{n^{2}})}^{- 1 / 2}$

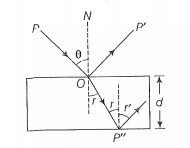
Step 2: Find the phase difference.

Phase difference = $∆ ϕ = \frac{2 π}{T} \times ∆ t = \frac{2 πnd}{λ} {(1 - \frac{\sin^{2} θ}{n^{2}})}^{- 1 / 2}$

$So, net phase difference = ∆ ϕ + π$
$= \frac{4 πd}{λ} {(1 - \frac{1}{n^{2}} \sin^{2} θ)}^{- 1 / 2} + π$

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions