Ncert Exercises & Solutions

For light diverging from a point source:

(a)	the wavefront is spherical.
(b)	the intensity decreases in proportion to the distance squared.
(c)	the wavefront is parabolic.
(d)	the intensity at the wavefront does not depend on the distance.

Choose the correct option:

1.	(a), (b)	2.	(a), (c)
3.	(b), (c)	4.	(c), (d)

(a, b) Hint: The shape of the wavefronts depends on the shape of the source.

Step 1: Find the shape of the wavefronts.
Consider the diagram in which light diverges from a point source (O).

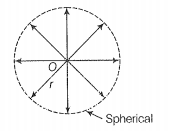
Due to the point source light propagates in all directions symmetrically and hence, the wavefront will be spherical as shown in the diagram.

Step 2: Find the intensity of wavefronts.
lf power of the source is P, then intensity of the source will be,

$I = \frac{P}{4 {πr}^{2}}$

Where, r is radius of the wavefront at any time.