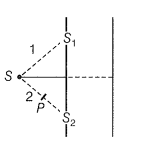
Hint: The intensity of the maxima or minima depends on the intensities of the individual interfering waves.

Step 1: Find the resultant amplitude without polariser.

A Resultant amplitude = A parallel (A)+ A perpendicular $\left(A_{\perp }\right)$

Without P:

$\begin{array}{rl}A& =A_{\perp }+A_{ll}\\ A& =A_{\perp }+A_{ll}\\ A_1=A_{\perp }^1+A_{\perp }^2& =A_{\perp }^0\sin (kx-\omega t)+A_{\perp }^0\sin (kx-\omega t+\varphi )\\ A_{\left|\right|}& =A_{\left|\right|}^{\left(1\right)}+A_{\left|\right|}^{\left(2\right)}\\ A_{\left|\right|}& =A_{\left|\right|}^0\left[\sin \right(kx-\omega t)+\sin (kx-\omega t+\varphi \left)\right]\end{array}$

where $A_{\perp }^0, A_{\left|\right|}^0$ are the amplitudes of either of the beam in perpendicular and parallel polarisations. 

 Step 2: Find the resultant intensity without polariser.

$\begin{array}{l}\ln tensity=\{{\left|A_{\perp }^0\right|}^2+{\left|A_{\left|\right|}^0\right|}^2\}\left[{\sin }^2\right(kx-\omega t)(1+{\cos }^2\varphi +2\sin \varphi )+{\sin }^2 (kx-\omega t){\sin }^2 \varphi ]\\ =\{{\left|A_{\perp }^0\right|}^2+{\left|A_{\left|\right|}^0\right|}^2\}\left(\frac{1}{2}\right)2(1+\cos \varphi )\\ =2{\left|A_{\perp }^0\right|}^2(1+\cos \varphi ), \mathrm{since}, {\left|A_{\perp }^0\right|}_{\text{av}}={\left|A_{\mathrm{ll}}^0\right|}_{\text{av}}\end{array}$

Step 3: Find the resultant intensity with polariser.

With P:

Assume $A_{\perp }^2$is blocked 

$Intensity ={(A_{\left|\right|}^1+A_{\left|\right|}^2)}^2+{\left(A_{\perp }^1\right)}^2 =\left|A_{\perp }^0\right(1+\cos \varphi )+|A_{\perp }^0{|}^2\times \frac{1}{2}$

Given ${\mathrm{I}}_0=4|{\mathrm{A}}_{\mathrm{bot}}^0{|}^2$=lntensity without polariser at principal maxima. 

lntensity at principal maxima with polariser = $\left|A_{\perp }^0{|}^2\right(2+\frac{1}{2})=\frac{5}{8}{l}_0$

intensity at first minima with polariser = $\left|A_{\perp }^0{|}^2\right(1-1)+\frac{|A_{\mathrm{II}}^0{|}^2}{2}=\frac{l_0}{8}$