Ncert Exercises & Solutions

14.9 A spring having a spring constant 1200 N/m is mounted on a horizontal table as shown in Fig. 14.24. A mass of 3 kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of 2.0 cm and released.

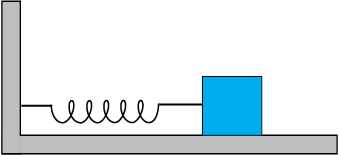
Fig. 14.24

Determine (i) the frequency of oscillations, (ii) maximum acceleration of the mass, and (iii) the maximum speed of the mass.

Spring constant, k = 1200 N m^{- 1}

Mass, m = 3 kg

Displacement, A = 2.0 cm = 0.02 cm

Frequency of oscillation ν, is given by the relation :

ν = \frac{1}{T} = \frac{1}{2 π} \sqrt{\frac{k}{m}}

where T is the time period

∴ ν = \frac{1}{2 \times 3.14} \sqrt{\frac{1200}{3}} = 3.18 Hz

Hence, the frequency of oscillations is 3.18 Hz .

Maximum acceleration (a) :

a = ω^{2} A

where ω = Angular frequency = \sqrt{\frac{k}{m}}

A = maximum displacement

a = \frac{k}{m} A = \frac{1200 \times 0.02}{3} = 8 {ms}^{- 2}

Hence, the maximum acceleration of the mass is 8.0 m / s^{2} .

Maximum velocity, v_{\max} = Aω = A \sqrt{\frac{k}{m}} = 0.02 \times \sqrt{\frac{1200}{3}} = 0.4 m / s

Hence, the maximum velocity of the mass is 0.4 m / s .

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions