14.12 Plot the corresponding reference circle for each of the following simple harmonic motions. Indicate the initial (t =0) position of the particle, the radius of the circle, and the angular speed of the rotating particle. For simplicity, the sense of rotation may be fixed to be anticlockwise in every case: (x is in cm and t is in s).
(a) x = –2sin(3t+π/3)
(b) x = cos(π/6 – t)
(c) x = 3sin2πt+π/4)
(d) x = 2cosπt
(a)
The motion of the particle is plotted as shown in the following figure.
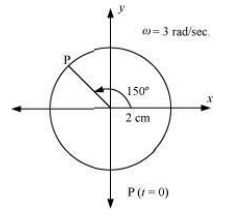
(b)
The motion of the particle is plotted as shown in the following figure.
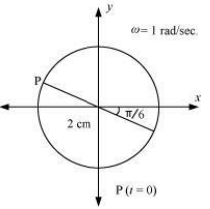
(c)
Comparing it with the standard SHM equation:
Then we get:
Amplitude, A = 3 cm
The motion of the particle is plotted as shown in the following figure.
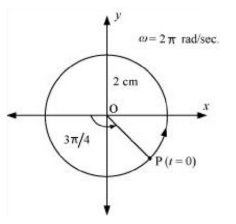
(d)
x = 2cos πt
Comparing it with the standard SHM equation: ,
then we get:
Amplitude, A = 2 cm
Phase angle, Φ = 0
Angular velocity, ω = π rad/s
The motion of the particle is plotted as shown in the following figure.
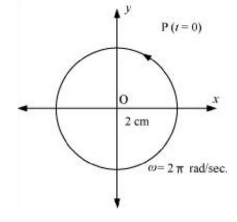

© 2025 GoodEd Technologies Pvt. Ltd.