Ncert Exercises & Solutions

The container shown in the figure has two chambers, separated by a partition, of volumes $V_{1}$ =2.0 L and $V_{2}$ =3.0 L. The chambers contain $μ_{1}$ =4.0 mole and $μ_{2}$ =5.0 mole of a gas at pressures $p_{1}$ =1.00 atm and $p_{2}$ =2.00 atm. Calculate the pressure after the partition is removed and the mixture attains equilibrium.

Hint: The total no. of molecules will remain the same.

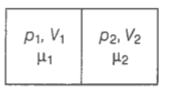
Consider the diagram,
Given,

V_{1} = 2.0 L, V_{2} = 30 L

μ_{1} = 40 m o l, μ_{2} = 50 m o l

p_{1} = 1.00 a t m, p_{2} = 2.00 a t m

Step 1: Find the relation between the pressure, volume and the total energy of the gas.

For chamber 1,

p_{1} V_{1} = μ_{1} R T_{1}

For chamber 2,

p_{2} V_{2} = μ_{2} R T_{2}

When the partition is removed the gasses get mixed without any loss of energy. The mixture now attains a common equilibrium pressure and the total volume of the system is the sum of the volume of individual chambers

V_{1} a n d V_{2}

So,

μ = μ_{1} + μ_{2}, V = V_{1} + V_{2}

From the kinetic theory of gases,

For 1 mole,

p V = \frac{2}{3} E

[E=translational kinetic energy]

For

μ_{1}

moles,

p_{1} V_{1} = \frac{2}{3} μ_{1} E_{1}

For

μ_{2}

moles,

p_{2} V_{2} = \frac{2}{3} μ_{2} E_{2}

The total energy is,

(μ_{1} E_{1} + μ_{2} E_{2}) = \frac{3}{2} (p_{1} V_{1} + p_{2} V_{2})

Step 2: Find the final pressure of the chamber.

From the above relation,

p V = \frac{2}{3} E_{t o t a l} = \frac{2}{3} μ E_{p e r m o l e}

p (V_{1} + V_{2}) = \frac{2}{3} \times \frac{3}{2} (p_{1} V_{1} + p_{2} V_{2})

p = \frac{p_{1} V_{1} + p_{2} V_{2}}{V_{1} + V_{2}}

= (\frac{1.00 \times 2.0 + 2.00 \times 30}{2.0 + 3.0}) a t m

= \frac{8.0}{5.0} = 160 a t m

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions