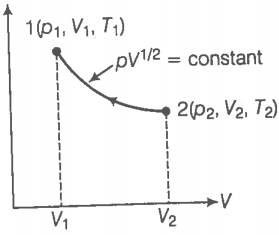
Consider a p-V diagram in which the path followed by one mole of a perfect gas in a cylindrical container is shown in the figure.
(a) Find the work done when the gas is taken from state 1 to state 2.
(b) What is the ratio of temperatures if ?
(c) Given the internal energy for one mole of gas at temperature T is (3/2)RT, find the heat supplied to the gas when it is taken from state 1 to 2 with .

© 2025 GoodEd Technologies Pvt. Ltd.