Ncert Exercises & Solutions

A cycle followed by an engine (made of one mole of a perfect gas in a cylinder with a piston) is shown in the figure.

A to B: volume constant

B to C: adiabatic

C to D: volume constant

D to A: adiabatic

$V_{C} = V_{D} = 2 V_{A} = 2 V_{B}$

(a) In which part of the cycle, the heat is supplied to the engine from outside?

(b) In which part of the cycle heat is being given to the surrounding by the engine?

(c) What is the work done by the engine in one cycle? Write your answer in term of $p_{A}, p_{B}, V_{A}$ ?
(d) What is the efficiency of the engine?

$(γ = \frac{5}{3}$ for the gas), ( $C_{V} = \frac{3}{2}$ R for one mole $)$

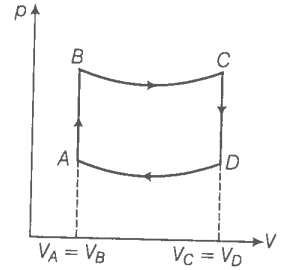
Hint: Use the first law of thermodynamics.

(a) Step 1: Find if the work is zero and dU > 0 in any process.

For the process AB,

dV = 0

\Rightarrow

dW = 0 (

∵

volume is constant)

dQ = dU+ dW = dU

\Rightarrow

dQ = dU = Change in internal energy.

Hence, in this process, the heat supplied is utilised to increase the internal energy of the system.

Since, p

= (\frac{n R}{V})

T, in isochoric process,

T \propto p

. So the temperature increases with increases of pressure in process AB which in turn increases the internal energy of the system ie., dU > 0. This implies that dQ > 0. So the heat is supplied to the system in process AB.

(b) Step 2: Find if the work is zero and dU < 0 in any process.

For the process CD, the volume is constant but the pressure decreases. Hence, the temperature also decreases. So the heat is given to the surroundings.

To calculate the work done by the engine in one cycle, we calculate the work done in each part separately.

W_{A B} = \int_{A}^{B} p d V = 0, W_{C D} = \int_{V_{C}}^{V_{D}} p d V = 0 (∵ d V = 0)

W_{B C} = \int_{V_{B}}^{V_{C}} p d V = k \int_{V_{B}}^{V_{C}} \frac{d V}{V^{γ}} = \frac{k}{1 - γ} {[V^{1 - γ}]}_{V_{B}}^{V_{C}}

= \frac{1}{1 - γ} {[p V]}_{V_{B}}^{V_{C}} = \frac{(p_{C} V_{C} - p_{B} V_{B})}{1 - γ}

Similarly,

W_{D A} = \frac{p_{A} V_{A} - p_{D} V_{D}}{1 - γ}

[

∵

BC and DA are adiabatic processes]

∵

B and C lie on adiabatic curve BC.

∴ p_{B} {V_{B}}^{γ} = p_{C} {V_{C}}^{γ}

p_{C} = p_{B} {(\frac{V_{B}}{V_{C}})}^{γ} = p_{B} {(\frac{1}{2})}^{γ} = 2^{- γ} p_{B}

Similarly,

p_{D} = 2^{- y} p_{A}

Total work done by the engine in one cycle ABCDA,

W = W_{A B} + W_{B C} + W_{C D} + W_{D A} = W_{B C} + W_{D A}

= \frac{(p_{C} V_{C} - p_{B} V_{B})}{1 - γ} + \frac{(p_{A} V_{A} - p_{D} V_{D})}{1 - γ}

W = \frac{1}{1 - γ} [2^{- γ} p_{B} (2 V_{B}) - p_{B} V_{B} + p_{A} V_{B} - 2^{- γ} p_{B} (2 V_{B})]

= \frac{1}{1 - γ} [p_{B} V_{B} (2^{- γ + 1} - 1) - p_{A} V_{B} (2^{- γ + 1} - 1)]

= \frac{1}{1 - γ} (2^{1 - γ} - 1) (p_{B} - p_{A}) V_{A}

= \frac{3}{2} [1 - {(\frac{1}{2})}^{2 / 3}] (p_{B} - p_{A}) V_{A}

(d) Step 4: Find the efficiency of the engine.

The heat supplied during the process AB,

d Q_{A B} = d U_{A B} = n C_{V} ∆ T = \frac{3}{2} n R ∆ T = \frac{3}{2} (p_{B} - p_{A}) V_{A}

The efficiency of the engine,

η = \frac{W}{Q} = \frac{\frac{3}{2} [1 - {(\frac{1}{2})}^{2 / 3}] (p_{B} - p_{A}) V_{A}}{\frac{3}{2} (p_{B} - p_{A}) V_{A}} = [1 - {(\frac{1}{2})}^{2 / 3}]

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions