Ncert Exercises & Solutions

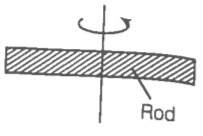
A uniform metallic rod rotates about its perpendicular bisector with the constant angular speed. If it is heated uniformly to raise its temperature slightly,

1. its speed of rotation increases

2. its speed of rotation decreases

3. its speed of rotation remains the same

4. its speed increases because its moment of inertia increases

(b) Hint: Apply the concept of conservation of angular momentum.

Step 1: Find the relation between the initial and final moment of inertia.

As the rod is heated, it expands. No external torque is acting on the system so angular momentum should be conserved.

L=Angular momentum=I

ω

= constant

\Rightarrow I_{1} ω_{1} = I_{2} ω_{2}

Due to the expansion of the rod

I_{2} > I_{1}

Step 2: Find the relation between initial and final angular velocities.

\Rightarrow \frac{ω_{2}}{ω_{1}} = \frac{I_{1}}{I_{2}} < 1

\Rightarrow ω_{2} < ω_{1}

So, angular velocity (speed of rotation) decreases.

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions