Ncert Exercises & Solutions

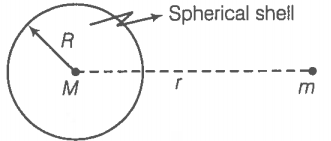
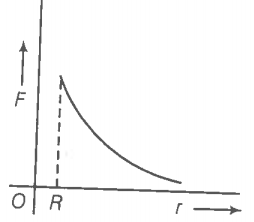
The gravitational force between a hollow spherical shell (of radius R and uniform density) and a point mass is F. Show the nature of F versus r graph where r is the distance of the point from the centre of the hollow spherical shell of uniform density.

Hint: The value of gravitational field varies with the distance from the centre of the shell.

Step 1: Find the force on a point due to the shell.

Consider the diagram, the density of the shell is constant. Let it is

ρ

Massof the shell = (density) x (volume)

= ρ \times \frac{4}{3} {πR}^{3} = M

As the density of the shell is uniform, it can be treated as a point mass placed at its centre for a point outside the shell. Therefore,

F = gravitational force between M and

m = \frac{G M m}{r^{2}}

F=0 for r < R (i.e., force inside the shell is zero)

= \frac{G M}{r^{2}} f o r r \geq R

Step 2: Draw the graph.

The variation of F versus r is shown in the diagram.

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions