Ncert Exercises & Solutions

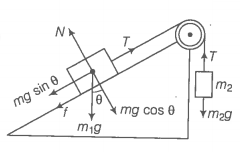
Mass \(m_{1}\) moves on a slope making an angle \(\theta\) with the horizontal and is attached to mass \(m_{2}\) by a string passing over a frictionless pulley as shown in the figure. The coefficient of friction between \(m_{1}\) and the sloping surface is \(\mu\).

(a)	If \(m_{2} > m_{1} \text{sin} ⁡ \theta \), the body will move up the plane.
(b)	If \(m_{2} > m_{1} (\text{sin} ⁡ \theta +\mu \text{cos} \theta)\), the body will move up the plane.
(c)	If \(m_{2} < m_{1} (\text{sin} ⁡ \theta +\mu \text{cos} \theta)\), the body will move up the plane.
(d)	If \(m_{2} < m_{1} (\text{sin} ⁡ \theta -\mu \text{cos} \theta)\), the body will move down the plane.

Which of the following statement/s is/are true?

1.	(a), (d)	2.	(a), (c)
3.	(c), (d)	4.	(b), (d)

(b, d) Hint: Apply Newton's laws of motion.

Let

m_{1}

moves up the plane, Different forces involved are shown in the diagram.

\begin{array}{l} N = Normal reaction \\ f = Frictional force \\ T = Tension in the string \\ f = μN = {μm}_{1} gcos θ \end{array}

Step 1: Find if the second body moves down.

\begin{array}{l} For the system (m_{1} + m_{2}) to move up \\ \begin{matrix} m_{2} g - (m_{1} gsin θ + f) > 0 \\ m_{2} g - (m_{1} gsin θ + {μm}_{1} gcos θ) > 0 \\ m_{2} > m_{1} (\sin θ + μcos θ) \end{matrix} \end{array}

Hence, option (b) is correct.

Step 2: Find if the first body moves down.
Let the body moves down the plane, in this case, f acts up the plane.

Hence,

\begin{array}{l} m_{1} gsin θ - f > m_{2} g \\ \Rightarrow m_{1} gsin θ - {μm}_{1} gcos θ > m_{2} g \\ \Rightarrow m_{1} (\sin θ - μcos θ) > m_{2} \\ \Rightarrow m_{2} < m_{1} (\sin θ - μcos θ) \end{array}

Hence, option (d) is correct.

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions