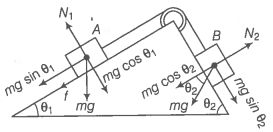
In figure a body \(A\) of mass \(m\) slides on a plane inclined at angle \(\left(\theta_{1}\right)\) to the horizontal and \(\mu\) is the coefficient of friction between \(A\) and the plane. \(A\) is connected by a light string passing over a frictionless pulley to another body \(B,\) also of mass \(m\), sliding on a frictionless plane inclined at an angle \(\left(\theta_{2}\right)\) to the horizontal.

| (a) | A will never move up the plane |
| (b) | A will just start moving up the plane when \(\mu = \dfrac{{\sin} \left(\theta\right)_{2} - {\sin} \left(\theta\right)_{1}}{{\cos} \left(\theta\right)_{1}}\) |
| (c) | For \(A\) to move up the plane, \(\left(\theta\right)_{2}\) must always be greater than \(\left(\theta\right)_{1}\) |
| (d) | \(B\) will always slide down with a constant speed |
Which of the following statement/s is/are true?
| 1. | (b, c) | 2. | (c, d) |
| 3. | (a, c) | 4. | (a, d) |

© 2025 GoodEd Technologies Pvt. Ltd.