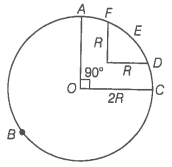
Q. 37 A racing car travels on a track (without banking) ABCDEFA. ABC is a circular arc of radius 2 R. CD and FA are straight paths of length R and DEF is a circular arc of radius R = 100 m. The coefficient of friction on the road is = 0.1. The maximum speed of the car is 50 m/s. Find the minimum time for completing one round.

© 2026 GoodEd Technologies Pvt. Ltd.