3.11 Conductivity of 0.00241 M acetic acid is 7.896 × 10–5 S cm–1. Calculate its molar conductivity. If 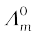 for acetic acid is 390.5 S cm2 mol–1, what is its dissociation constant?
for acetic acid is 390.5 S cm2 mol–1, what is its dissociation constant?

© 2026 GoodEd Technologies Pvt. Ltd.