The increased growth per unit time is termed as growth rate. Thus, rate of growth can be expressed mathematically. An organism, or a part of the organism can produce more cells in a variety of ways.
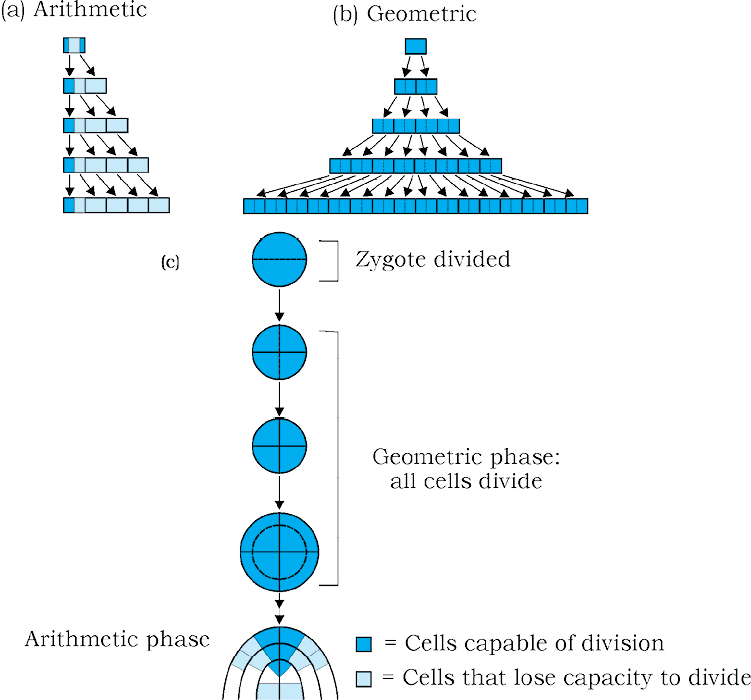
Figure15.4 Diagrammatic representation of : (a) Arithmetic (b) Geometric growth and (c) Stages during embryo development showing geometric and arithematic phases
The growth rate shows an increase that may be arithmetic or geometrical (Figure 15.4).
In arithmetic growth, following mitotic cell division, only one daughter cell continues to divide while the other differentiates and matures. The simplest expression of arithmetic growth is exemplified by a root elongating at a constant rate. Look at Figure 15.5.
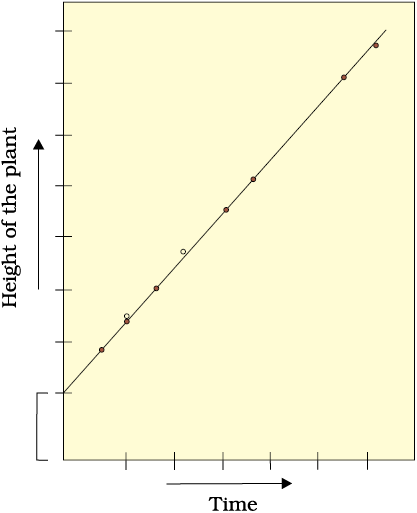
On plotting the length of the organ against time, a linear curve is obtained. Mathematically, it is expressed as
Lt = L0 + rt
Lt = length at time ‘t’
L0 = length at time ‘zero’
r = growth rate / elongation per unit time.
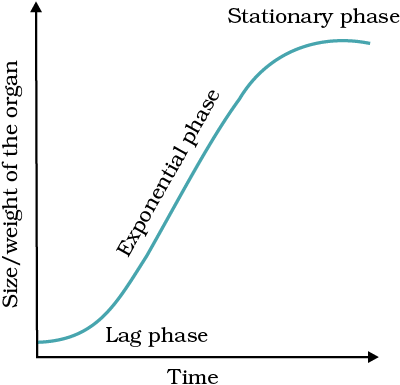
Let us now see what happens in geometrical growth. In most systems, the initial growth is slow (lag phase), and it increases rapidly thereafter – at an exponential rate (log or exponential phase). Here, both the progeny cells following mitotic cell division retain the ability to divide and continue to do so. However, with limited nutrient supply, the growth slows down leading to a stationary phase. If we plot the parameter of growth against time, we get a typical sigmoid or S-curve (Figure 15.6). A sigmoid curve is a characteristic of living organism growing in a natural environment. It is typical for all cells, tissues and organs of a plant. Can you think of more similar examples? What kind of a curve can you expect in a tree showing seasonal activities?
The exponential growth can be expressed as
W1 = W0 ert
W1 = final size (weight, height, number etc.)
W0 = initial size at the beginning of the period
r = growth rate
t = time of growth
e = base of natural logarithms
Here, r is the relative growth rate and is also the measure of the ability of the plant to produce new plant material, referred to as efficiency index. Hence, the final size of W1depends on the initial size, W0.
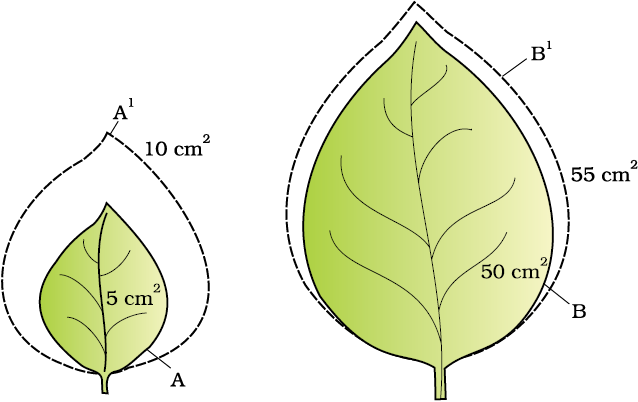
Quantitative comparisons between the growth of living system can also be made in two ways : (i) measurement and the comparison of total growth per unit time is called the absolute growth rate. (ii) The growth of the given system per unit time expressed on a common basis, e.g., per unit initial parameter is called the relative growth rate. In Figure 15.7 two leaves, A and B, are drawn that are of different sizes but shows absolute increase in area in the given time to give leaves, A1 and B1. However, one of them shows much higher relative growth rate. Which one and why?