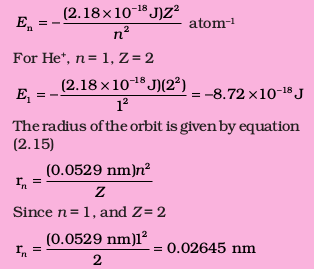Neils Bohr (1913) was the first to explain quantitatively the general features of the structure of hydrogen atom and its spectrum. He used Planck’s concept of quantisation of energy. Though the theory is not the modern quantum mechanics, it can still be used to rationalize many points in the atomic structure and spectra. Bohr’s model for hydrogen atom is based on the following postulates:
i) The electron in the hydrogen atom can move around the nucleus in a circular path of fixed radius and energy. These paths are called orbits, stationary states or allowed energy states. These orbits are arranged concentrically around the nucleus.
ii) The energy of an electron in the orbit does not change with time. However, the electron will move from a lower stationary state to a higher stationary state when required amount of energy is absorbed by the electron or energy is emitted when electron moves from higher stationary state to lower stationary state (equation 2.16). The energy change does not take place in a continuous manner.
Angular Momentum
Just as linear momentum is the product of mass (m) and linear velocity (v), angular momentum is the product of moment of inertia (I) and angular velocity (ω). For an electron of mass me, moving in a circular path of radius r around the nucleus,
angular momentum = I × ω
Since I = mer2, and ω = v/r where v is the linear velocity,
∴angular momentum = mer2 × v/r = mevr
iii) The frequency of radiation absorbed or emitted when transition occurs between two stationary states that differ in energy by ∆E, is given by:
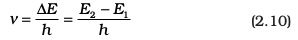
Where E1 and E2 are the energies of the lower and higher allowed energy states respectively. This expression is commonly known as Bohr’s frequency rule.
iv) The angular momentum of an electron is quantised. In a given stationary state it can be expressed as in equation (2.11)
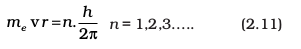
Where me is the mass of electron, v is the velocity and r is the radius of the orbit in which electron is moving.
Thus an electron can move only in those orbits for which its angular momentum is integral multiple of h/2π. That means angular momentum is quantised. Radiation is emitted or obsorbed only when transition of electron takes place from one quantised value of angular momentum to another. Therefore, Maxwell’s electromagnetic theory does not apply here that is why only certain fixed orbits are allowed.
The details regarding the derivation of energies of the stationary states used by Bohr, are quite complicated and will be discussed in higher classes. However, according to Bohr’s theory for hydrogen atom:
a) The stationary states for electron are numbered n = 1,2,3.......... These integral numbers (Section 2.6.2) are known as Principal quantum numbers.
b) The radii of the stationary states are expressed as: rn = n2 a0 (2.12)
where a0 = 52.9 pm. Thus the radius of the first stationary state, called the Bohr orbit, is 52.9 pm. Normally the electron in the hydrogen atom is found in this orbit (that is n=1). As n increases the value of r will increase. In other words the electron will be present away from the nucleus.
c) The most important property associated with the electron, is the energy of its stationary state. It is given by the expression.

where RH is called Rydberg constant and its value is 2.18×10–18 J. The energy of the lowest state, also called as the ground state, is
E1 = –2.18×10–18 (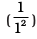 ) = –2.18×10–18 J. The energy of the stationary state for n = 2, will
) = –2.18×10–18 J. The energy of the stationary state for n = 2, will
be : E2 = –2.18×10–18J (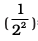 )= –0.545×10–18 J. Fig. 2.11 depicts the energies of different stationary states or energy levels of hydrogen atom. This representation is called an energy level diagram.
)= –0.545×10–18 J. Fig. 2.11 depicts the energies of different stationary states or energy levels of hydrogen atom. This representation is called an energy level diagram.

When the electron is free from the influence of nucleus, the energy is taken as zero. The electron in this situation is associated with the stationary state of Principal Quantum number = n = ∞ and is called as ionized hydrogen atom. When the electron is attracted by the nucleus and is present in orbit n, the energy is emitted and its energy is lowered. That is the reason for the presence of negative sign in equation (2.13) and depicts its stability relative to the reference state of zero energy and n = ∞.
What does the negative electronic energy (En) for hydrogen atom mean?
The energy of the electron in a hydrogen atom has a negative sign for all possible orbits (eq. 2.13). What does this negative sign convey? This negative sign means that the energy of the electron in the atom is lower than the energy of a free electron at rest. A free electron at rest is an electron that is infinitely far away from the nucleus and is assigned the energy value of zero. Mathematically, this corresponds to setting n equal to infinity in the equation (2.13) so that E∞=0. As the electron gets closer to the nucleus (as n decreases), En becomes larger in absolute value and more and more negative. The most negative energy value is given by n=1 which corresponds to the most stable orbit. We call this the ground state.
d) Bohr’s theory can also be applied to the ions containing only one electron, similar to that present in hydrogen atom. For example, He+ Li2+, Be3+ and so on. The energies of the stationary states associated with these kinds of ions (also known as hydrogen like species) are given by the expression.
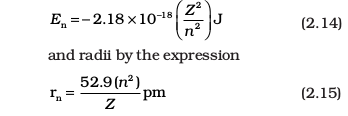
where Z is the atomic number and has values 2,3 for the helium and lithium atoms respectively. From the above equations, it is evident that the value of energy becomes more negative and that of radius becomes smaller with increase of Z . This means that electron will be tightly bound to the nucleus.
e) It is also possible to calculate the velocities of electrons moving in these orbits. Although the precise equation is not given here, qualitatively the magnitude of velocity of electron increases with increase of positive charge on the nucleus and decreases with increase of principal quantum number.
2.4.1 Explanation of Line Spectrum of Hydrogen
Line spectrum observed in case of hydrogen atom, as mentioned in section 2.3.3, can be explained quantitatively using Bohr’s model. According to assumption 2, radiation (energy) is absorbed if the electron moves from the orbit of smaller Principal quantum number to the orbit of higher Principal quantum number, whereas the radiation (energy) is emitted if the electron moves from higher orbit to lower orbit. The energy gap between the two orbits is given by equation (2.16)
∆E = Ef – Ei (2.16)
Combining equations (2.13) and (2.16)
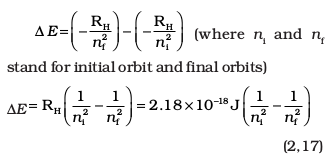
The frequency (ν ) associated with the absorption and emission of the photon can be evaluated by using equation (2.18)

In case of absorption spectrum, nf > ni and the term in the parenthesis is positive and energy is absorbed. On the other hand in case of emission spectrum ni > nf , ∆ E is negative and energy is released.
The expression (2.17) is similar to that used by Rydberg (2.9) derived empirically using the experimental data available at that time. Further, each spectral line, whether in absorption or emission spectrum, can be associated to the particular transition in hydrogen atom. In case of large number of hydrogen atoms, different possible transitions can be observed and thus leading to large number of spectral lines. The brightness or intensity of spectral lines depends upon the number of photons of same wavelength or frequency absorbed or emitted.
Problem 2.10
What are the frequency and wavelength of a photon emitted during a transition from n = 5 state to the n = 2 state in the hydrogen atom?
Solution
Since ni = 5 and nf = 2, this transition gives rise to a spectral line in the visible region of the Balmer series. From equation (2.17)
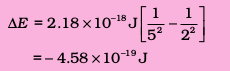
It is an emission energy
The frequency of the photon (taking
energy in terms of magnitude) is given by
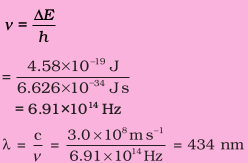
Problem 2.11
Calculate the energy associated with the first orbit of He+. What is the radius of this orbit?
Solution