Disproportionation reactions are a special type of redox reactions. In a disproportionation reaction an element in one oxidation state is simultaneously oxidised and reduced. One of the reacting substances in a disproportionation reaction always contains an element that can exist in at least three oxidation states. The element in the form of reacting substance is in the intermediate oxidation state; and both higher and lower oxidation states of that element are formed in the reaction. The decomposition of hydrogen peroxide is a familiar example of the reaction, where oxygen experiences disproportionation.
+1 –1 +1 –2 0
2H2O2 (aq) → 2H2O(l) + O2(g) (8.45)
Here the oxygen of peroxide, which is present in –1 state, is converted to zero oxidation state in O2 and decreases to –2 oxidation state in H2O.
Phosphorous, sulphur and chlorine undergo disproportionation in the alkaline medium as shown below :
0 –3 +1
P4(s) + 3OH–(aq)+ 3H2O(l) → PH3(g) + 3H2PO2– (aq) (8.46)
0 –2 +2
S8(s) + 12OH– (aq) → 4S2– (aq) + 2S2O32–(aq) + 6H2O(l) (8.47)
0 +1 –1
Cl2 (g) + 2OH– (aq) → ClO– (aq) + Cl– (aq) + H2O (l) (8.48)
The reaction (8.48) describes the formation of household bleaching agents. The hypochlorite ion (ClO–) formed in the reaction oxidises the colour-bearing stains of the substances to colourless compounds.
It is of interest to mention here that whereas bromine and iodine follow the same trend as exhibited by chlorine in reaction (8.48), fluorine shows deviation from this behaviour when it reacts with alkali. The reaction that takes place in the case of fluorine is as follows:
2 F2(g) + 2OH–(aq) → 2 F–(aq) + OF2(g) + H2O(l) (8.49)
(It is to be noted with care that fluorine in reaction (8.49) will undoubtedly attack water to produce some oxygen also). This departure shown by fluorine is not surprising for us as we know the limitation of fluorine that, being the most electronegative element, it cannot exhibit any positive oxidation state. This means that among halogens, fluorine does not show a disproportionation tendency.
Problem 8.5
Which of the following species, do not show disproportionation reaction and why ?
ClO–, ClO2–, ClO3– and ClO4 –
Also write reaction for each of the species that disproportionates.
Solution
Among the oxoanions of chlorine listed above, ClO4– does not disproportionate because in this oxoanion chlorine is present in its highest oxidation state that is, +7. The disproportionation reactions for the other three oxoanions of chlorine are as follows:
+1 –1 +5
3ClO– → 2Cl– + ClO–3
+3 +5 –1
6 ClO2– 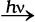 4ClO3– + 2Cl–
4ClO3– + 2Cl–
+5 –1 +7
4ClO3– → Cl– + 3 ClO4–
Problem 8.6
Suggest a scheme of classification of the following redox reactions
(a) N2 (g) + O2 (g) → 2 NO (g)
(b) 2Pb(NO3)2(s) → 2PbO(s) + 4 NO2 (g) + O2 (g)
(c) NaH(s) + H2O(l) → NaOH(aq) + H2 (g)
(d) 2NO2(g) + 2OH–(aq) → NO2–(aq) + NO3– (aq)+H2O(l)
Solution
In reaction (a), the compound nitric oxide is formed by the combination of the elemental substances, nitrogen and oxygen; therefore, this is an example of combination redox reactions. The reaction (b) involves the breaking down of lead nitrate into three components; therefore, this is categorised under decomposition redox reaction. In reaction (c), hydrogen of water has been displaced by hydride ion into dihydrogen gas. Therefore, this may be called as displacement redox reaction. The reaction (d) involves disproportionation of NO2
(+4 state) into NO2– (+3 state) and NO3– (+5 state). Therefore reaction (d) is an example of disproportionation redox reaction.
Sometimes, we come across with certain compounds in which the oxidation number of a particular element in the compound is in fraction. Examples are:
C3O2 [where oxidation number of carbon is (4/3)],
Br3O8 [where oxidation number of bromine is (16/3)]
and Na2S4O6 (where oxidation number of sulphur is 2.5).
We know that the idea of fractional oxidation number is unconvincing to us, because electrons are never shared/transferred in fraction. Actually this fractional oxidation state is the average oxidation state of the element under examination and the structural parameters reveal that the element for whom fractional oxidation state is realised is present in different oxidation states. Structure of the species C3O2, Br3O8 and S4O62– reveal the following bonding situations:
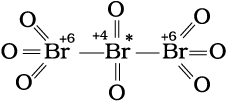
O = C = C*= C = O
Structure of C3O2
(carbon suboxide)
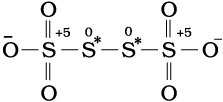
Structure of S4O62– (tetrathionate ion)
The element marked with asterisk in each species is exhibiting the different oxidation state (oxidation number) from rest of the atoms of the same element in each of the species. This reveals that in C3O2, two carbon atoms are present in +2 oxidation state each, whereas the third one is present in zero oxidation state and the average is 4/3. However, the realistic picture is +2 for two terminal carbons and zero for the middle carbon. Likewise in Br3O8, each of the two terminal bromine atoms are present in +6 oxidation state and the middle bromine is present in +4 oxidation state. Once again the average, that is different from reality, is
16/3. In the same fashion, in the species S4O62–, each of the two extreme sulphurs exhibits oxidation state of +5 and the two middle sulphurs as zero. The average of four oxidation numbers of sulphurs of the S4O62– is 2.5, whereas the reality being + 5,0,0 and +5 oxidation number respectively for each sulphur.
We may thus, in general, conclude that the idea of fractional oxidation state should be taken with care and the reality is revealed by the structures only. Further, whenever we come across with fractional oxidation state of any particular element in any species, we must understand that this is the average oxidation number only. In reality (revealed by structures only), the element in that particular species is present in more than one whole number oxidation states. Fe3O4, Mn3O4, Pb3O4 are some of the other examples of the compounds, which are mixed oxides, where we come across with fractional oxidation states of the metal atom. However, the oxidation states may be in fraction as in O2+ and O2– where it is +½ and –½ respectively.
Problem 8.7
Why do the following reactions proceed differently ?
Pb3O4 + 8HCl → 3PbCl2 + Cl2 + 4H2O and
Pb3O4 + 4HNO3 → 2Pb(NO3)2 + PbO2 + 2H2O
Solution
Pb3O4 is actually a stoichiometric mixture of 2 mol of PbO and 1 mol of PbO2. In PbO2, lead is present in +4 oxidation state, whereas the stable oxidation state of lead in PbO is +2. PbO2 thus can act as an oxidant (oxidising agent) and, therefore, can oxidise Cl– ion of HCl into chlorine. We may also keep in mind that PbO is a basic oxide. Therefore, the reaction
Pb3O4 + 8HCl → 3PbCl2 + Cl2 + 4H2O
can be splitted into two reactions namely:
2PbO + 4HCl → 2PbCl2 + 2H2O
(acid-base reaction)
+4 –1 +2 0
PbO2 + 4HCl → PbCl2 + Cl2 +2H2O (redox reaction)
Since HNO3 itself is an oxidising agent therefore, it is unlikely that the reaction may occur between PbO2 and HNO3. However, the acid-base reaction occurs between PbO and HNO3 as:
2PbO + 4HNO3 → 2Pb(NO3)2 + 2H2O
It is the passive nature of PbO2 against HNO3 that makes the reaction different from the one that follows with HCl.
8.3.2 Balancing of Redox Reactions
Two methods are used to balance chemical equations for redox processes. One of these methods is based on the change in the oxidation number of reducing agent and the oxidising agent and the other method is based on splitting the redox reaction into two half reactions — one involving oxidation and the other involving reduction. Both these methods are in use and the choice of their use rests with the individual using them.
(a) Oxidation Number Method: In writing equations for oxidation-reduction reactions, just as for other reactions, the compositions and formulas must be known for the substances that react and for the products that are formed. The oxidation number method is now best illustrated in the following steps:
Step 1: Write the correct formula for each reactant and product.
Step 2: Identify atoms which undergo change in oxidation number in the reaction by assigning the oxidation number to all elements in the reaction.
Step 3: Calculate the increase or decrease in the oxidation number per atom and for the entire molecule/ion in which it occurs. If these are not equal then multiply by suitable number so that these become equal. (If you realise that two substances are reduced and nothing is oxidised or vice-versa, something is wrong. Either the formulas of reactants or products are wrong or the oxidation numbers have not been assigned properly).
Step 4: Ascertain the involvement of ions if the reaction is taking place in water, add H+ or OH– ions to the expression on the appropriate side so that the total ionic charges of reactants and products are equal. If the reaction is carried out in acidic solution, use H+ ions in the equation; if in basic solution, use OH– ions.
Step 5: Make the numbers of hydrogen atoms in the expression on the two sides equal by adding water (H2O) molecules to the reactants or products. Now, also check the number of oxygen atoms. If there are the same number of oxygen atoms in the reactants and products, the equation then represents the balanced redox reaction.
Let us now explain the steps involved in the method with the help of a few problems given below:
Problem 8.8
Write the net ionic equation for the reaction of potassium dichromate(VI), K2Cr2O7 with sodium sulphite, Na2SO3, in an acid solution to give chromium(III) ion and the sulphate ion.
Solution
Step 1: The skeletal ionic equation is:
Cr2O72–(aq) + SO32–(aq) → Cr3+(aq) + SO42–(aq)
Step 2: Assign oxidation numbers for Cr and S
+6 –2 +4 –2 +3 +6 –2
Cr2O72–(aq) + SO32–(aq) → Cr(aq)+SO42–(aq)
This indicates that the dichromate ion is the oxidant and the sulphite ion is the reductant.
Step 3: Calculate the increase and decrease of oxidation number, and make them equal: from step-2 we can notice that there is change in oxidation state of chromium and sulphur. Oxidation state of chromium changes form +6 to +3. There is decrease of +3 in oxidation state of chromium on right hand side of the equation. Oxidation state of sulphur changes from +4 to +6. There is an increase of +2 in the oxidation state of sulphur on right hand side. To make the increase and decrease of oxidation state equal, place numeral 2 before cromium ion on right hand side and numeral 3 before sulphate ion on right hand side and balance the chromium and sulphur atoms on both the sides of the equation. Thus we get
+6 –2 +4 –2 +3 +6 –2
Cr2O72–(aq) + 3SO32– (aq) → 2Cr3+ (aq) + 3SO42– (aq)
Step 4: As the reaction occurs in the acidic medium, and further the ionic charges are not equal on both the sides, add 8H+ on the left to make ionic charges equal
Cr2O72–(aq) + 3SO32–(aq)+ 8H+→ 2Cr3+(aq) + 3SO42– (aq)
Step 5: Finally, count the hydrogen atoms, and add appropriate number of water molecules (i.e., 4H2O) on the right to achieve balanced redox change.
Cr2O72–(aq) + 3SO32– (aq)+ 8H+ (aq) → 2Cr3+ (aq) + 3SO42– (aq) +4H2O (l)
Problem 8.9
Permanganate ion reacts with bromide ion in basic medium to give manganese dioxide and bromate ion. Write the balanced ionic equation for the reaction.
Solution
Step 1: The skeletal ionic equation is :
MnO4–(aq) + Br–(aq) → MnO2(s) + BrO3– (aq)
Step 2: Assign oxidation numbers for Mn and Br
+7 –1 +4 +5
MnO4–(aq) + Br–(aq) →MnO2 (s) + BrO3– (aq)
this indicates that permanganate ion is the oxidant and bromide ion is the reductant.
Step 3: Calculate the increase and decrease of oxidation number, and make the increase equal to the decrease.
+7 –1 +4 +5
2MnO4–(aq) + Br–(aq) → 2MnO2(s) + BrO3–(aq)
Step 4: As the reaction occurs in the basic medium, and the ionic charges are not equal on both sides, add 2 OH– ions on the right to make ionic charges equal.
2MnO4– (aq) + Br– (aq) → 2MnO2(s) + BrO3–(aq) + 2OH–(aq)
Step 5: Finally, count the hydrogen atoms and add appropriate number of water molecules (i.e. one H2O molecule) on the left side to achieve balanced redox change.
2MnO4–(aq) + Br–(aq) + H2O(l) → 2MnO2(s) + BrO3– (aq) + 2OH–(aq)
In this method, the two half equations are balanced separately and then added together to give balanced equation.
Suppose we are to balance the equation showing the oxidation of Fe2+ ions to Fe3+ ions by dichromate ions (Cr2O7)2– in acidic medium, wherein, Cr2O72– ions are reduced to Cr3+ ions. The following steps are involved in this task.
Step 1: Produce unbalanced equation for the reaction in ionic form :
Fe2+(aq) + Cr2O72– (aq) → Fe3+ (aq) + Cr3+(aq) (8.50)
Step 2: Separate the equation into half-reactions:
+2 +3
Oxidation half : Fe2+ (aq) → Fe3+(aq) (8.51)
+6 –2 +3
Reduction half : Cr2O72–(aq) → Cr3+(aq) (8.52)
Step 3: Balance the atoms other than O and H in each half reaction individually. Here the oxidation half reaction is already balanced with respect to Fe atoms. For the reduction half reaction, we multiply the Cr3+ by 2 to balance Cr atoms.
Cr2O72–(aq) → 2Cr3+(aq) (8.53)
Step 4: For reactions occurring in acidic medium, add H2O to balance O atoms and H+ to balance H atoms.
Thus, we get :
Cr2O72– (aq) + 14H+ (aq) → 2Cr3+(aq) + 7H2O (l) (8.54)
Step 5: Add electrons to one side of the half reaction to balance the charges. If need be, make the number of electrons equal in the two half reactions by multiplying one or both half reactions by appropriate number.
The oxidation half reaction is thus rewritten to balance the charge:
Fe2+ (aq) → Fe3+ (aq) + e– (8.55)
Now in the reduction half reaction there are net twelve positive charges on the left hand side and only six positive charges on the right hand side. Therefore, we add six electrons on the left side.
Cr2O72– (aq) + 14H+ (aq) + 6e– → 2Cr3+(aq) + 7H2O (l) (8.56)
To equalise the number of electrons in both the half reactions, we multiply the oxidation half reaction by 6 and write as :
6Fe2+ (aq) → 6Fe3+(aq) + 6e– (8.57)
Step 6: We add the two half reactions to achieve the overall reaction and cancel the electrons on each side. This gives the net ionic equation as :
6Fe2+(aq) + Cr2O72–(aq) + 14H+(aq) → 6 Fe3+(aq) + 2Cr3+(aq) + 7H2O(l) (8.58)
Step 7: Verify that the equation contains the same type and number of atoms and the same charges on both sides of the equation. This last check reveals that the equation is fully balanced with respect to number of atoms and the charges.
For the reaction in a basic medium, first balance the atoms as is done in acidic medium. Then for each H+ ion, add an equal number of OH– ions to both sides of the equation. Where H+ and OH– appear on the same side of the equation, combine these to give H2O.
Problem 8.10
Permanganate(VII) ion, MnO4– in basic solution oxidises iodide ion, I– to produce molecular iodine (I2) and manganese (IV) oxide (MnO2). Write a balanced ionic equation to represent this redox reaction.
Solution
Step 1: First we write the skeletal ionic equation, which is
MnO4– (aq) + I– (aq) → MnO2(s) + I2(s)
Step 2: The two half-reactions are:
–1 0
Oxidation half : I–(aq) → I2 (s)
+7 +4
Reduction half: MnO4–(aq) → MnO2(s)
Step 3: To balance the I atoms in the oxidation half reaction, we rewrite it as:
2I– (aq) → I2 (s)
Step 4: To balance the O atoms in the reduction half reaction, we add two water molecules on the right:
MnO4– (aq) → MnO2 (s) + 2 H2O (l)
To balance the H atoms, we add four H+ ions on the left:
MnO4– (aq) + 4 H+ (aq) → MnO2(s) + 2H2O (l)
As the reaction takes place in a basic solution, therefore, for four H+ ions, we add four OH– ions to both sides of the equation:
MnO4– (aq) + 4H+ (aq) + 4OH–(aq) → MnO2 (s) + 2 H2O(l) + 4OH– (aq)
Replacing the H+ and OH– ions with water, the resultant equation is:
MnO4– (aq) + 2H2O (l) → MnO2 (s) + 4 OH– (aq)
Step 5: In this step we balance the charges of the two half-reactions in the manner depicted as:
2I– (aq) → I2 (s) + 2e–
MnO4–(aq) + 2H2O(l) + 3e– → MnO2(s) + 4OH–(aq)
Now to equalise the number of electrons, we multiply the oxidation half-reaction by 3 and the reduction half-reaction by 2.
6I–(aq) → 3I2 (s) + 6e–
2 MnO4– (aq) + 4H2O (l) +6e– → 2MnO2(s) + 8OH– (aq)
Step 6: Add two half-reactions to obtain the net reactions after cancelling electrons on both sides.
6I–(aq) + 2MnO4–(aq) + 4H2O(l) → 3I2(s) + 2MnO2(s) + 8OH–(aq)
Step 7: A final verification shows that the equation is balanced in respect of the number of atoms and charges on both sides.
8.3.3 Redox Reactions as the Basis for Titrations
In acid-base systems we come across with a titration method for finding out the strength of one solution against the other using a pH sensitive indicator. Similarly, in redox systems, the titration method can be adopted to determine the strength of a reductant/oxidant using a redox sensitive indicator. The usage of indicators in redox titration is illustrated below:
(i) In one situation, the reagent itself is intensely coloured, e.g., permanganate ion, MnO4–. Here MnO4– acts as the self indicator. The visible end point in this case is achieved after the last of the reductant (Fe2+ or C2O42–) is oxidised and the first lasting tinge of pink colour appears at MnO4– concentration as low as 10–6 mol dm–3 (10–6 mol L–1). This ensures a minimal ‘overshoot’ in colour beyond the equivalence point, the point where the reductant and the oxidant are equal in terms of their mole stoichiometry.
(ii) If there is no dramatic auto-colour change (as with MnO4– titration), there are indicators which are oxidised immediately after the last bit of the reactant is consumed, producing a dramatic colour change. The best example is afforded by Cr2O72–, which is not a self-indicator, but oxidises the indicator substance diphenylamine just after the equivalence point to produce an intense blue colour, thus signalling the end point.
(iii) There is yet another method which is interesting and quite common. Its use is restricted to those reagents which are able to oxidise I– ions, say, for example, Cu(II):
2Cu2+(aq) + 4I–(aq) → Cu2I2(s) + I2(aq) (8.59)
This method relies on the facts that iodine itself gives an intense blue colour with starch and has a very specific reaction with thiosulphate ions (S2O32–), which too is a redox reaction:
I2(aq) + 2 S2O32–(aq)→2I–(aq) + S4O62–(aq) (8.60)
I2, though insoluble in water, remains in solution containing KI as KI3.
On addition of starch after the liberation of iodine from the reaction of Cu2+ ions on iodide ions, an intense blue colour appears. This colour disappears as soon as the iodine is consumed by the thiosulphate ions. Thus, the end-point can easily be tracked and the rest is the stoichiometric calculation only.
8.3.4 Limitations of Concept of Oxidation Number
As you have observed in the above discussion, the concept of redox processes has been evolving with time. This process of evolution is continuing. In fact, in recent past the oxidation process is visualised as a decrease in electron density and reduction process as an increase in electron density around the atom(s) involved in the reaction.