13.4 KINETIC THEORY OF AN IDEAL GAS

13.4.1 Pressure of an Ideal Gas

Fig. 13.3 Experimental T-V curves (solid lines) for CO2 at three pressures compared with Charles’ law (dotted lines). T is in units of 300 K and V in units of 0.13 litres.

We next consider some examples which give us information about the volume occupied by
the molecules and the volume of a single molecule.

Example 13.1 The density of water is 1000 kg m–3. The density of water vapour at 100 °C and 1 atm pressure is 0.6 kg m–3. The volume of a molecule multiplied by the total number gives ,what is called, molecular volume. Estimate the ratio (or fraction) of the molecular volume to the total volume occupied by the water vapour under the above conditions of temperature and pressure.

Answer For a given mass of water molecules, the density is less if volume is large. So the volume of the vapour is 1000/0.6 = 1/(6 ×10 -4 ) times larger. If densities of bulk water and water molecules are same, then the fraction of molecular volume to the total volume in liquid state is 1. As volume in vapour state has increased, the fractional volume is less by the same amount, i.e. 6×10-4. t

Example 13.2 Estimate the volume of a water molecule using the data in Example 13.1.

Answer In the liquid (or solid) phase, the molecules of water are quite closely packed. The density of water molecule may therefore, be regarded as roughly equal to the density of bulk water = 1000 kg m–3. To estimate the volume of a water molecule, we need to know the mass of a single water molecule. We know that 1 mole of water has a mass approximately equal to

(2 + 16)g = 18 g = 0.018 kg.

Since 1 mole contains about 6 × 1023 molecules (Avogadro’s number), the mass of a molecule of water is (0.018)/(6 × 1023) kg =
3 × 10–26 kg. Therefore, a rough estimate of the volume of a water molecule is as follows :

Volume of a water molecule

= (3 × 10–26 kg)/ (1000 kg m–3)

= 3 × 10–29 m3

= (4/3) π (Radius)3

Hence, Radius ≈ 2 ×10-10 m = 2 Å t

Example 13.3 What is the average distance between atoms (interatomic distance) in water? Use the data given in Examples 13.1 and 13.2.

Answer : A given mass of water in vapour state has 1.67×103 times the volume of the same mass of water in liquid state (Ex. 13.1). This is also the increase in the amount of volume available for each molecule of water. When volume increases by 103 times the radius increases by V1/3 or 10 times, i.e., 10 × 2 Å = 20 Å. So the average distance is 2 × 20 = 40 Å. t

Example 13.4 A vessel contains two non-reactive gases : neon (monatomic) and oxygen (diatomic). The ratio of their partial pressures is 3:2. Estimate the ratio of (i) number of molecules and (ii) mass density of neon and oxygen in the vessel. Atomic mass of Ne = 20.2 u, molecular mass of O2 = 32.0 u.

Answer Partial pressure of a gas in a mixture is the pressure it would have for the same volume and temperature if it alone occupied the vessel. (The total pressure of a mixture of non-reactive gases is the sum of partial pressures due to its constituent gases.) Each gas (assumed ideal) obeys the gas law. Since V and T are common to the two gases, we have P1V = µ 1 RT and P2V = µ2 RT, i.e. (P1/P2) = (µ1 / µ2). Here 1 and 2 refer to neon and oxygen respectively. Since (P1/P2) = (3/2) (given), (µ1/ µ2) = 3/2.

(i) By definition µ1 = (N1/NA ) and µ2 = (N2/NA) where N1 and N2 are the number of molecules of 1 and 2, and NA is the Avogadro’s number.

Therefore, (N1/N2) = (µ1 / µ2) = 3/2.

(ii) We can also write µ1 = (m1/M1) and µ2 =
(m2/M2) where m1 and m2 are the masses of 1 and 2; and M1 and M2 are their molecular masses. (Both m1 and M1; as well as m2 and M2 should be expressed in the same units). If ρ1 and ρ2 are the mass densities of 1 and 2 respectively, we have

t

13.4 KINETIC THEORY OF AN IDEAL GAS

Kinetic theory of gases is based on the molecular picture of matter. A given amount of gas is a collection of a large number of molecules (typically of the order of Avogadro’s number) that are in incessant random motion. At ordinary pressure and temperature, the average distance between molecules is a factor of 10 or more than the typical size of a molecule (2 Å). Thus, interaction between molecules is negligible and we can assume that they move freely in straight lines according to Newton’s first law. However, occasionally, they come close to each other, experience intermolecular forces and their velocities change. These interactions are called collisions. The molecules collide incessantly against each other or with the walls and change their velocities. The collisions are considered to be elastic. We can derive an expression for the pressure of a gas based on the kinetic theory.

We begin with the idea that molecules of a gas are in incessant random motion, colliding against one another and with the walls of the container. All collisions between molecules among themselves or between molecules and the walls are elastic. This implies that total kinetic energy is conserved. The total momentum is conserved as usual.

13.4.1 Pressure of an Ideal Gas

Consider a gas enclosed in a cube of side l. Take the axes to be parallel to the sides of the cube, as shown in Fig. 13.4. A molecule with velocity (vx, vy, vz ) hits the planar wall parallel to yz-plane of area A (= l2). Since the collision is elastic, the molecule rebounds with the same velocity; its y and z components of velocity do not change in the collision but the x-component reverses sign. That is, the velocity after collision is
(-vx, vy, vz ) . The change in momentum of the molecule is: –mvx – (mvx) = – 2mvx . By the principle of conservation of momentum, the momentum imparted to the wall in the collision = 2mvx .

Fig. 13.4 Elastic collision of a gas molecule with the wall of the container.

Fig. 13.4 Elastic collision of a gas molecule with the wall of the container.

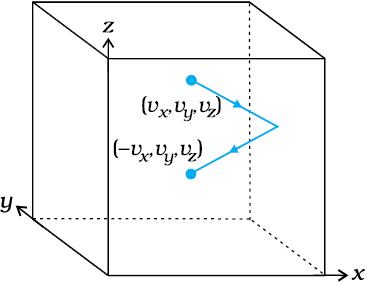
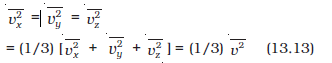To calculate the force (and pressure) on the wall, we need to calculate momentum imparted to the wall per unit time. In a small time interval $∆t$, a molecule with x-component of velocity v_x will hit the wall if it is within the distance v_x $∆t$ from the wall. That is, all molecules within the volume Av_x $∆t$ only can hit the wall in time Dt. But, on the average, half of these are moving towards the wall and the other half away from the wall. Thus, the number of molecules with velocity (vx, vy, vz ) hitting the wall in time $∆t$ is

½A vx $∆t$ n, where n is the number of molecules per unit volume. The total momentum transferred to the wall by these molecules in time $∆t$ is:

Q = (2mvx) (½ n A vx $∆t$ )                                                (13.10)

The force on the wall is the rate of momentum transfer Q/$∆t$ and pressure is force per unit area :

P = Q /(A $∆t$) = n m vx 2 (3.11)

Actually, all molecules in a gas do not have the same velocity; there is a distribution in velocities. The above equation, therefore, stands for pressure due to the group of molecules with speed vx in the x-direction and n stands for the number density of that group of molecules. The total pressure is obtained by summing over the contribution due to all groups:

P = n m vx2   (13.12)

where $\overline{v_x^2}$ is the average of vx2 .  Now the gas is isotropic, i.e. there is no preferred direction of velocity of the molecules in the vessel.

Therefore, by symmetry,

where v is the speed and  v2 denotes the mean of the squared speed. Thus

P = (1/3) n m $\overline{v_{}^2}$   (13.14)

Some remarks on this derivation. First, though we choose the container to be a cube, the shape of the vessel really is immaterial. For a vessel of arbitrary shape, we can always choose a small infinitesimal (planar) area and carry through the steps above. Notice that both A and $∆t$ do not appear in the final result. By Pascal’s law, given in Ch. 10, pressure in one portion of the gas in equilibrium is the same as anywhere else. Second, we have ignored any collisions inthe derivation. Though this assumption is difficult to justify rigorously, we can qualitatively see that it will not lead to erroneous results.

The number of molecules hitting the wall in time Dt was found to be ½ n Avx$∆t$. Now the collisions are random and the gas is in a steady state. Thus, if a molecule with velocity (vx, vy, vz ) acquires a different velocity due to collision with some molecule, there will always be some other molecule with a different initial velocity which after a collision acquires the velocity (vx, vy, vz ).

If this were not so, the distribution of velocities would not remain steady. In any case we are finding $\overline{v_x^2}$ . Thus, on the whole, molecular collisions (if they are not too frequent and the time spent in a collision is negligible compared to time between collisions) will not affect the calculation above.