15.6.1 Standing waves and normal modes

 We considered above reflection at one boundary. But there are familiar situations (a string fixed at either end or an air column in a pipe with either end closed) in which reflection takes place at two or more boundaries. In a string, for example, a wave travelling in one direction will get reflected at one end, which in turn will travel and get reflected from the other end. This will go on until there is a steady wave pattern set up on the string. Such wave patterns are called standing waves or stationary waves. To see this mathematically, consider a wave travelling along the positive direction of x-axis and a reflected wave of the same amplitude and wavelength in the negative direction of x-axis. From Eqs. (15.2) and (15.4), with φ = 0, we get:

y₁(x, t) = a sin (kx – ωt)

y₂(x, t) = a sin (kx + ωt)

The resultant wave on the string is, according to the principle of superposition:

y (x, t) = y₁(x, t) + y₂(x, t)

= a [sin (kx – ωt) + sin (kx + ωt)]

Using the familiar trignometric identity

Sin (A+B) + Sin (A–B) = 2 sin A cosB we get,

y (x, t) = 2a sin kx cos ωt (15.37)

Note the important difference in the wave pattern described by Eq. (15.37) from that described by Eq. (15.2) or Eq. (15.4). The terms kx and ωt appear separately, not in the combination kx - ωt. The amplitude of this wave is 2a sin kx. Thus, in this wave pattern, the amplitude varies from point-to-point, but each element of the string oscillates with the same angular frequency ω or time period. There is no phase difference between oscillations of different elements of the wave. The string as a whole vibrates in phase with differing amplitudes at different points. The wave pattern is neither moving to the right nor to the left. Hence, they are called standing or stationary waves. The amplitude is fixed at a given location but, as remarked earlier, it is different at different locations. The points at which the amplitude is zero (i.e., where there is no motion at all) are nodes; the points at which the amplitude is the largest are called antinodes. Fig. 15.12 shows a stationary wave pattern resulting from superposition of two travelling waves in opposite directions.

 The most significant feature of stationary waves is that the boundary conditions constrain the possible wavelengths or frequencies of vibration of the system. The system cannot oscillate with any arbitrary frequency (contrast this with a harmonic travelling wave), but is characterised by a set of natural frequencies or normal modes of oscillation. Let us determine these normal modes for a stretched string fixed at both ends.

First, from Eq. (15.37), the positions of nodes (where the amplitude is zero) are given by

sin kx = 0 .

which implies

kx = nπ; n = 0, 1, 2, 3, ...

Since, k = 2π/λ , we get

x = $\frac{n\lambda }{2}$ ; n = 0, 1, 2, 3, ... (15.38)

Clearly, the distance between any two successive nodes is $\frac{\lambda }{2}$. In the same way, the positions of antinodes (where the amplitude is the largest) are given by the largest value of sin kx :

sin kx = 1

which implies

kx = (n + ½) π ; n = 0, 1, 2, 3, ...

With k = 2π/λ, we get

x = (n + ½)λ/2 ; n = 0, 1, 2, 3, ... (15.39)

Fig. 15.12 Stationary waves arising from superposition of two harmonic waves travelling in opposite directions. Note that the positions of zero displacement (nodes) remain fixed at all times.

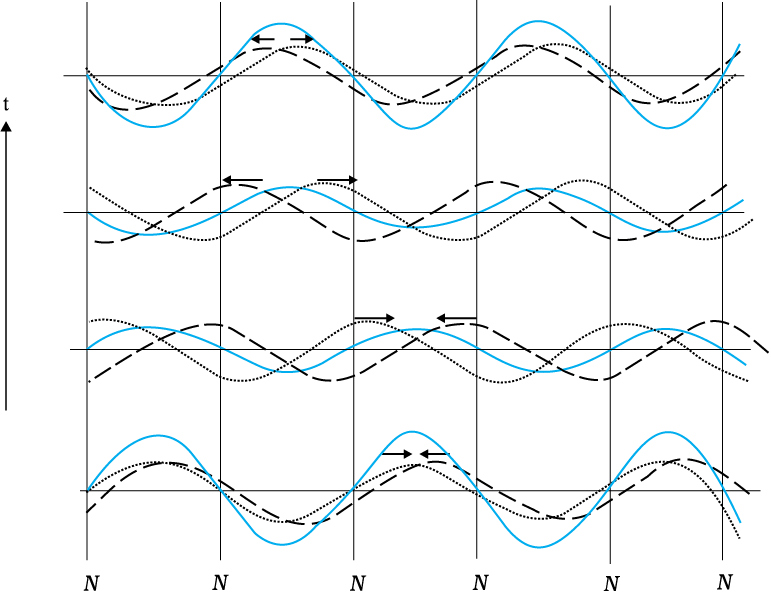
Again the distance between any two consecutive antinodes is $\frac{\lambda }{2}$. Eq. (15.38) can be applied to the case of a stretched string of length L fixed at both ends. Taking one end to be at x = 0, the boundary conditions are that x = 0 and x = L are positions of nodes. The x = 0 condition is already satisfied. The x = L node condition requires that the length L is related to λ by

L = n $\frac{\lambda }{2}$; n = 1, 2, 3, ... (15.40)

Thus, the possible wavelengths of stationary waves are constrained by the relation

λ = $\frac{2L}{n}$; n = 1, 2, 3, … (15.41)

with corresponding frequencies

v = $\frac{nv}{2L}$, for n = 1, 2, 3, (15.42)

 We have thus obtained the natural frequencies - the normal modes of oscillation of the system. The lowest possible natural frequency of a system is called its fundamental mode or the first harmonic. For the stretched string fixed at either end it is given by v = $\frac{v}{2L}$, corresponding to n = 1 of Eq. (15.42). Here v is the speed of wave determined by the properties of the medium. The n = 2 frequency is called the second harmonic; n = 3 is the third harmonic and so on. We can label the various harmonics by the symbol νn ( n = 1, 2, ...).

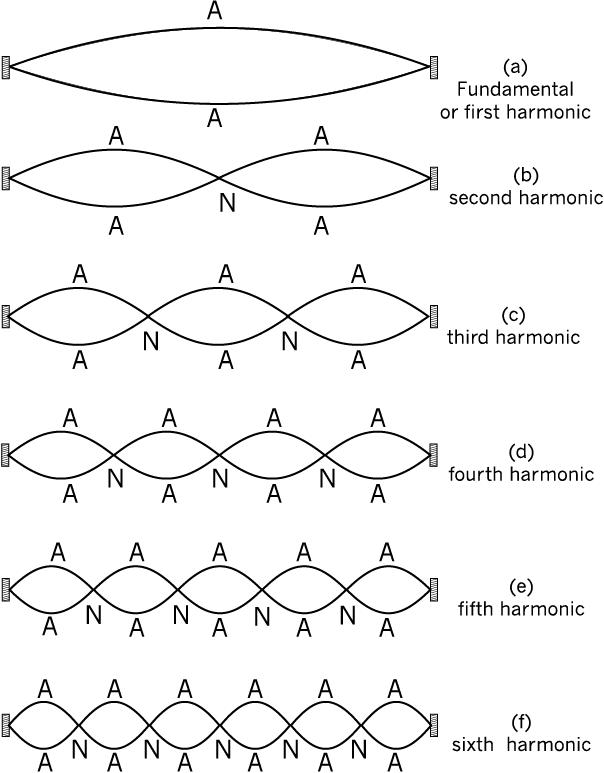
Fig. 15.13 The first six harmonics of vibrations of a stretched string fixed at both ends.

Fig. 15.13 shows the first six harmonics of a stretched string fixed at either end. A string need not vibrate in one of these modes only. Generally, the vibration of a string will be a superposition of different modes; some modes may be more strongly excited and some less. Musical instruments like sitar or violin are based on this principle. Where the string is plucked or bowed, determines which modes are more prominent than others.

Let us next consider normal modes of oscillation of an air column with one end closed and the other open. A glass tube partially filled with water illustrates this system. The end in contact with water is a node, while the open end is an antinode. At the node the pressure changes are the largest, while the displacement is minimum (zero). At the open end - the antinode, it is just the other way - least pressure change and maximum amplitude of displacement. Taking the end in contact with water to be x = 0, the node condition (Eq. 15.38) is already satisfied. If the other end x = L is an antinode, Eq. (15.39) gives

L = $\left(n+\frac{1}{2}\right)\frac{\lambda }{2}$, for n = 0, 1, 2, 3, …

The possible wavelengths are then restricted by the relation :

λ = $\frac{2L}{\left(n+1/2\right)}$, for n = 0, 1, 2, 3,... (15.43)

The normal modes – the natural frequencies – of the system are

ν = $\left(n+\frac{1}{2}\right)\frac{v}{2L}$; n = 0, 1, 2, 3, ... (15.44)

The fundamental frequency corresponds to n = 0, and is given by $\frac{v}{4L}$ . The higher frequencies are odd harmonics, i.e., odd multiples of the fundamental frequency : 3$\frac{v}{4L}$, 5$\frac{v}{4L}$, etc.

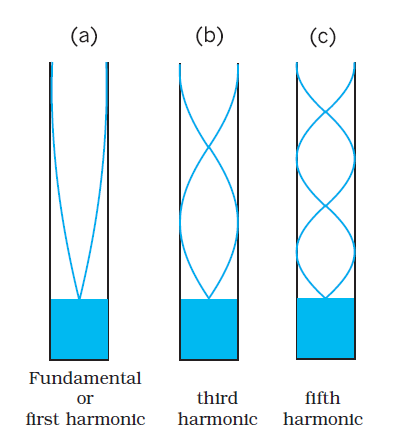
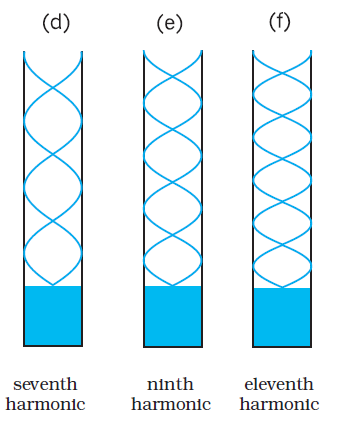
Fig. 15.14 Normal modes of an air column open at one end and closed at the other end. Only the odd harmonics are seen to be possible.

Fig. 15.14 shows the first six odd harmonics of air column with one end closed and the other open. For a pipe open at both ends, each end is an antinode. It is then easily seen that an open air column at both ends generates all harmonics (See Fig. 15.15).

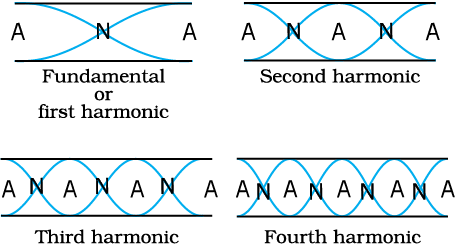
Fig. 15.15 Standing waves in an open pipe, first four harmonics are depicted.

The systems above, strings and air columns, can also undergo forced oscillations (Chapter 14). If the external frequency is close to one of the natural frequencies, the system shows resonance.

Normal modes of a circular membrane rigidly clamped to the circumference as in a tabla are determined by the boundary condition that no point on the circumference of the membrane vibrates. Estimation of the frequencies of normal modes of this system is more complex. This problem involves wave propagation in two dimensions. However, the underlying physics is the same.

Example 15.5 A pipe, 30.0 cm long, is open at both ends. Which harmonic mode of the pipe resonates a 1.1 kHz source? Will resonance with the same source be observed if one end of the pipe is closed ? Take the speed of sound in air as
330 m s^–1.

Answer

The first harmonic frequency is given by

ν₁ = $\frac{v}{{\lambda }_1}=\frac{v}{2L}$(open pipe)

where L is the length of the pipe. The frequency of its nth harmonic is:

ν_n = $\frac{n}{2L}$, for n = 1, 2, 3, ... (open pipe)

First few modes of an open pipe are shown in Fig. 15.15.

For L = 30.0 cm, v = 330 m s–1,

ν_n = $\frac{n 330\left(m{s}^{-1}\right)}{0.6\left(m\right)}$ = 550 n s^–1

Clearly, a source of frequency 1.1 kHz will resonate at v₂, i.e. the second harmonic.

Now if one end of the pipe is closed (Fig. 15.15), it follows from Eq. (14.50) that the fundamental frequency is

ν₁ = $\frac{v}{{\lambda }_1}=\frac{v}{4L}$ (pipe closed at one end)

and only the odd numbered harmonics are present :

ν₃ = $\frac{3v}{4L}$, ν₅ = $\frac{5v}{4L}$, and so on.

For L = 30 cm and v = 330 m s^–1, the fundamental frequency of the pipe closed at one end is 275 Hz and the source frequency corresponds to its fourth harmonic. Since this harmonic is not a possible mode, no resonance will be observed with the source, the moment one end is closed.