Earlier in the section, we have learnt that when particles are close-packed resulting in either ccp or hcp structure, two types of voids are generated. While the number of octahedral voids present in a lattice is equal to the number of close packed particles, the number of tetrahedral voids generated is twice this number. In ionic solids, the bigger ions (usually anions) form the close packed structure and the smaller ions (usually cations) occupy the voids. If the latter ion is small enough then tetrahedral voids are occupied, if bigger, then octahedral voids. All octahedral or tetrahedral voids are not occupied. In a given compound, the fraction of octahedral or tetrahedral voids that are occupied, depends upon the chemical formula of the compound, as can be seen from the following examples.
Example 1.1
A compound is formed by two elements X and Y. Atoms of the element Y (as anions) make ccp and those of the element X (as cations) occupy all the octahedral voids. What is the formula of the compound?
Solution
The ccp lattice is formed by the element Y. The number of octahedral voids generated would be equal to the number of atoms of Y present in it. Since all the octahedral voids are occupied by the atoms of X, their number would also be equal to that of the element Y. Thus, the atoms of elements X and Y are present in equal numbers or 1:1 ratio. Therefore, the formula of the compound is XY.
Example 1.2
Atoms of element B form hcp lattice and those of the element A occupy 2/3rd of tetrahedral voids. What is the formula of the compound formed by the elements A and B?
Solution
The number of tetrahedral voids formed is equal to twice the number of atoms of element B and only 2/3rd of these are occupied by the atoms of element A. Hence the ratio of the number of atoms of A and B is 2 × (2/3):1 or 4:3 and the formula of the compound is A4B3.
Locating Tetrahedral and Octahedral Voids
We know that close packed structures have both tetrahedral and octahedral voids. Let us take ccp (or fcc) structure and locate these voids in it.
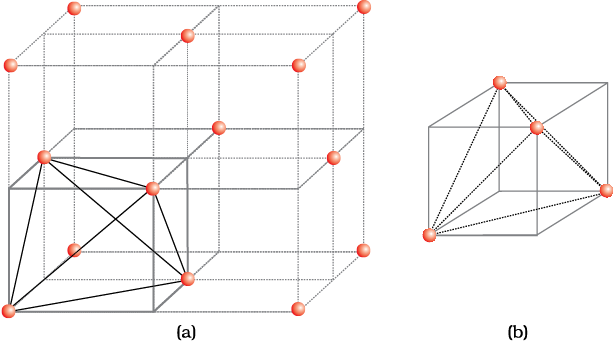
(a) Locating Tetrahedral Voids
Let us consider a unit cell of ccp or fcc lattice [Fig. 1(a)]. The unit cell is divided into eight small cubes.
Each small cube has atoms at alternate corners [Fig. 1(a)]. In all, each small cube has 4 atoms. When joined to each other, they make a regular tetrahedron. Thus, there is one tetrahedral void in each small cube and eight tetrahedral voids in total. Each of the eight small cubes have one void in one unit cell of ccp structure. We know that ccp structure has 4 atoms per unit cell. Thus, the number of tetrahedral voids is twice the number of atoms.
(b) Locating Octahedral Voids
Let us again consider a unit cell of ccp or fcc lattice [Fig. 2(a)]. The body centre of the cube, C is not occupied but it is surrounded by six atoms on face centres. If these face centres are joined, an octahedron is generated. Thus, this unit cell has one octahedral void at the body centre of the cube.
Besides the body centre, there is one octahedral void at the centre of each of the 12 edges [Fig. 2(b)]. It is surrounded by six atoms, four belonging to the same unit cell (2 on the corners and 2 on face centre) and two belonging to two adjacent unit cells. Since each edge of the cube is shared between four adjacent unit cells, so is the octahedral void located on it. Only th of each void belongs to a particular unit cell.
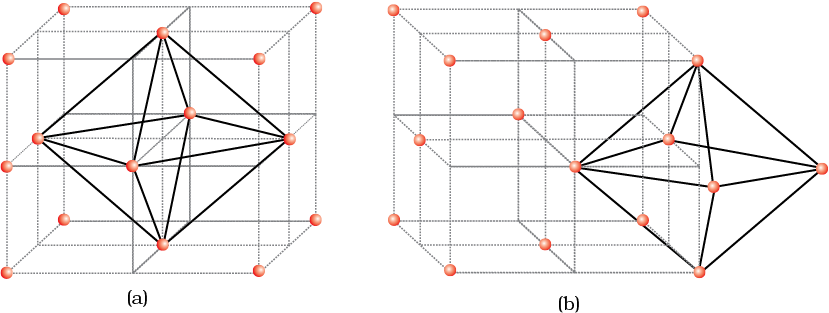
Fig. 2: Location of octahedral voids per unit cell of ccp or fcc lattice (a) at the body centre of the cube and (b) at the centre of each edge (only one such void is shown).
Thus in cubic close packed structure:
Octahedral void at the body-centre of the cube = 1
12 octahedral voids located at each edge and shared between four unit cells
=
∴ Total number of octahedral voids = 4
We know that in ccp structure, each unit cell has 4 atoms. Thus, the number of octahedral voids is equal to this number.