You may wonder why the notion of electric field has been introduced here at all. After all, for any system of charges, the measurable quantity is the force on a charge which can be directly determined using Coulomb’s law and the superposition principle [Eq. (1.5)]. Why then introduce this intermediate quantity called the electric field?
For electrostatics, the concept of electric field is convenient, but not really necessary. Electric field is an elegant way of characterising the electrical environment of a system of charges. Electric field at a point in the space around a system of charges tells you the force a unit positive test charge would experience if placed at that point (without disturbing the system). Electric field is a characteristic of the system of charges and is independent of the test charge that you place at a point to determine the field. The term field in physics generally refers to a quantity that is defined at every point in space and may vary from point to point. Electric field is a vector field, since force is a vector quantity.
The true physical significance of the concept of electric field, however, emerges only when we go beyond electrostatics and deal with time-dependent electromagnetic phenomena. Suppose we consider the force between two distant charges q1, q2 in accelerated motion. Now the greatest speed with which a signal or information can go from one point to another is c, the speed of light. Thus, the effect of any motion of q1 on q2 cannot arise instantaneously. There will be some time delay between the effect (force on q2) and the cause (motion of q1). It is precisely here that the notion of electric field (strictly, electromagnetic field) is natural and very useful. The field picture is this: the accelerated motion of charge q1 produces electromagnetic waves, which then propagate with the speed c, reach q2 and cause a force on q2. The notion of field elegantly accounts for the time delay. Thus, even though electric and magnetic fields can be detected only by their effects (forces) on charges, they are regarded as physical entities, not merely mathematical constructs. They have an independent dynamics of their own, i.e., they evolve according to laws of their own. They can also transport energy. Thus, a source of time-dependent electromagnetic fields, turned on for a short interval of time and then switched off, leaves behind propagating electromagnetic fields transporting energy. The concept of field was first introduced by Faraday and is now among the central concepts in physics.
Example 1.8 An electron falls through a distance of 1.5 cm in a uniform electric field of magnitude 2.0 × 104 N C–1 [Fig. 1.13(a)]. The direction of the field is reversed keeping its magnitude unchanged and a proton falls through the same distance [Fig. 1.13(b)]. Compute the time of fall in each case. Contrast the situation with that of ‘free fall under gravity’.
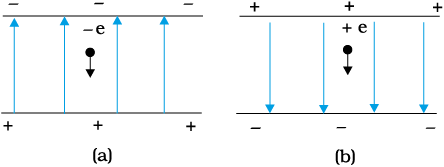
Solution In Fig. 1.13(a) the field is upward, so the negatively charged electron experiences a downward force of magnitude eE where E is the magnitude of the electric field. The acceleration of the electron is
ae = eE/me
where me is the mass of the electron.
Starting from rest, the time required by the electron to fall through a distance h is given by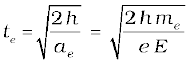
For e = 1.6 × 10–19C, me = 9.11 × 10–31 kg,
E = 2.0 × 104 N C–1, h = 1.5 × 10–2 m,
te = 2.9 × 10–9s
In Fig. 1.13 (b), the field is downward, and the positively charged proton experiences a downward force of magnitude eE. The acceleration of the proton is
ap = eE/mp
where mp is the mass of the proton; mp = 1.67 × 10–27 kg. The time of fall for the proton is
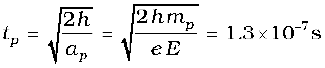
Thus, the heavier particle (proton) takes a greater time to fall through the same distance. This is in basic contrast to the situation of ‘free fall under gravity’ where the time of fall is independent of the mass of the body. Note that in this example we have ignored the acceleration due to gravity in calculating the time of fall. To see if this is justified, let us calculate the acceleration of the proton in the given electric field:
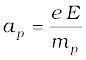
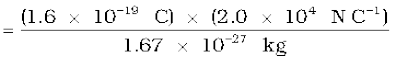
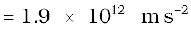
which is enormous compared to the value of g (9.8 m s–2), the acceleration due to gravity. The acceleration of the electron is even greater. Thus, the effect of acceleration due to gravity can be ignored in this example.
Example 1.9 Two point charges q1 and q2, of magnitude +10–8 C and –10–8 C, respectively, are placed 0.1 m apart. Calculate the electric fields at points A, B and C shown in Fig. 1.14.
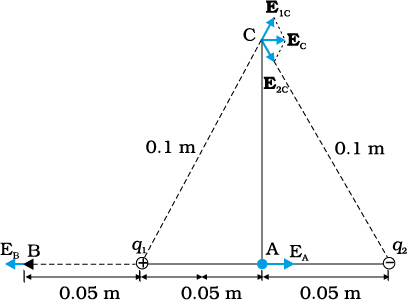
Figure 1.14
Solution The electric field vector E1A at A due to the positive charge q1 points towards the right and has a magnitude
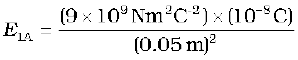= 3.6 × 104 N C–1
The electric field vector E2A at A due to the negative charge q2 points towards the right and has the same magnitude. Hence the magnitude of the total electric field EA at A is
EA = E1A + E2A = 7.2 × 104 N C–1
EA is directed toward the right.
The electric field vector E1B at B due to the positive charge q1 points towards the left and has a magnitude
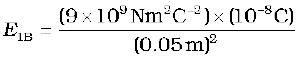= 3.6 × 104 N C–1
The electric field vector E2B at B due to the negative charge q2 points towards the right and has a magnitude
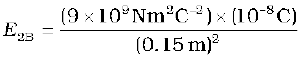= 4 × 103 N C–1
The magnitude of the total electric field at B is
EB = E1B – E2B = 3.2 × 104 N C–1
EB is directed towards the left.
The magnitude of each electric field vector at point C, due to charge q1 and q2 is
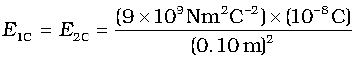= 9 × 103 N C–1
The directions in which these two vectors point are indicated in
Fig. 1.14. The resultant of these two vectors is
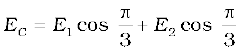= 9 × 103 N C–1
EC points towards the right.
© 2025 GoodEd Technologies Pvt. Ltd.
