1.15 Applications of Gauss’s Law

 The electric field due to a general charge distribution is, as seen above, given by Eq. (1.27). In practice, except for some special cases, the summation (or integration) involved in this equation cannot be carried out to give electric field at every point in space. For some symmetric charge configurations, however, it is possible to obtain the electric field in a simple way using the Gauss’s law. This is best understood by some examples.

1.15.1 Field due to an infinitely long straight uniformly charged wire

 Consider an infinitely long thin straight wire with uniform linear charge density λ. The wire is obviously an axis of symmetry. Suppose we take the radial vector from O to P and rotate it around the wire. The points P, P′, P′′ so obtained are completely equivalent with respect to the charged wire. This implies that the electric field must have the same magnitude at these points. The direction of electric field at every point must be radial (outward if λ > 0, inward if λ < 0). This is clear from Fig. 1.29.

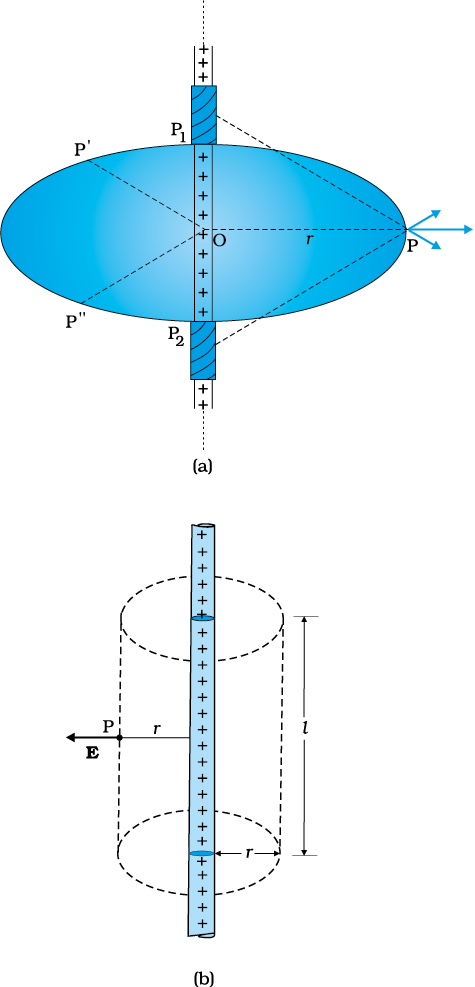
Figure 1.29 (a) Electric field due to an infinitely long thin straight wire is radial, (b) The Gaussian surface for a long thin wire of uniform linear charge density.

 Consider a pair of line elements P1 and P2 of the wire, as shown. The electric fields produced by the two elements of the pair when summed give a resultant electric field which is radial (the components normal to the radial vector cancel). This is true for any such pair and hence the total field at any point P is radial. Finally, since the wire is infinite, electric field does not depend on the position of P along the length of the wire. In short, the electric field is everywhere radial in the plane cutting the wire normally, and its magnitude depends only on the radial distance r.

To calculate the field, imagine a cylindrical Gaussian surface, as shown in the Fig. 1.29(b).Since the field is everywhere radial, flux through the two ends of the cylindrical Gaussian surface is zero. At the cylindrical part of the surface, E is normal to the surface at every point, and its magnitude is constant, since it depends only on r. The surface area of the curved part is 2πrl, where l is the length of the cylinder.

 Flux through the Gaussian surface

= flux through the curved cylindrical part of the surface

= E × 2πrl

The surface includes charge equal to λ l. Gauss’s law then gives

E × 2πrl = λl/ε0

i.e., E =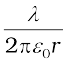

 Vectorially, E at any point is given by

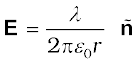(1.32)

where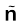is the radial unit vector in the plane normal to the wire passing through the point. E is directed outward if λ is positive and inward if λ is negative.

 Note that when we write a vector A as a scalar multiplied by a unit vector, i.e., as A = A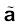, the scalar A is an algebraic number. It can be negative or positive. The direction of A will be the same as that of the unit vector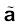if A > 0 and opposite to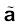if A < 0. When we want to restrict to non-negative values, we use the symboland call it the modulus of A. Thus,.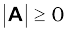

Also note that though only the charge enclosed by the surface (λl) was included above, the electric field E is due to the charge on the entire wire. Further, the assumption that the wire is infinitely long is crucial. Without this assumption, we cannot take E to be normal to the curved part of the cylindrical Gaussian surface. However, Eq. (1.32) is approximately true for electric field around the central portions of a long wire, where the end effects may be ignored.