The pattern of iron filings, i.e., the magnetic field lines gives us an approximate idea of the magnetic field B. We may at times be required to determine the magnitude of B accurately. This is done by placing a small compass needle of known magnetic moment m and moment of inertia I and allowing it to oscillate in the magnetic field. This arrangement is shown in Fig. 5.4(b).
The torque on the needle is [see Eq. (4.29)],
τ = m × B (5.3)
In magnitude τ = mB sinθ
Here τ is restoring torque and θ is the angle between m and B.
Therefore, in equilibrium 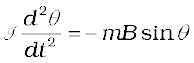
Negative sign with mB sinθ implies that restoring torque is in opposition to deflecting torque. For small values of θ in radians, we approximate
sin θ ≈ θ and get
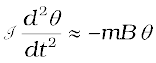
or, 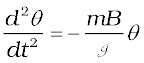
This represents a simple harmonic motion. The square of the angular frequency is ω2 = mB/I and the time period is,
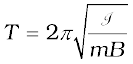 (5.4)
(5.4)
or 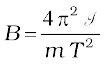 (5.5)
(5.5)
An expression for magnetic potential energy can also be obtained on lines similar to electrostatic potential energy.
The magnetic potential energy Um is given by
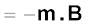 (5.6)
(5.6)
We have emphasised in Chapter 2 that the zero of potential energy can be fixed at one’s convenience. Taking the constant of integration to be zero means fixing the zero of potential energy at θ = 90°, i.e., when the needle is perpendicular to the field. Equation (5.6) shows that potential energy is minimum (= –mB) at θ = 0° (most stable position) and maximum (= +mB) at θ = 180° (most unstable position).
Example 5.1 In Fig. 5.4(b), the magnetic needle has magnetic moment 6.7 × 10–2 Am2 and moment of inertia I = 7.5 × 10–6 kg m2. It performs 10 complete oscillations in 6.70 s. What is the magnitude of the magnetic field?
Solution The time period of oscillation is,
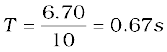
From Eq. (5.5)
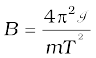
=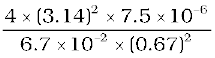
= 0.01 T
Example 5.2 A short bar magnet placed with its axis at 30° with an external field of 800 G experiences a torque of 0.016 Nm. (a) What is the magnetic moment of the magnet? (b) What is the work done in moving it from its most stable to most unstable position? (c) The bar magnet is replaced by a solenoid of cross-sectional area 2 × 10–4 m2 and 1000 turns, but of the same magnetic moment. Determine the current flowing through the solenoid.
Solution
(a) From Eq. (5.3), τ = m B sin θ, θ = 30°, hence sinθ =1/2.
Thus, 0.016 = m × (800 × 10–4T) × (1/2)
m = 160 × 2/800 = 0.40 A m2
(b) From Eq. (5.6), the most stable position is θ = 0° and the most unstable position is θ = 180°. Work done is given by
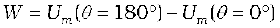
= 2 m B = 2 × 0.40 × 800 × 10–4 = 0.064 J
(c) From Eq. (4.30), ms = NIA. From part (a), ms = 0.40 A m2
0.40 = 1000 × I × 2 × 10–4
I = 0.40 × 104/(1000 × 2) = 2A
Example 5.3
(a) What happens if a bar magnet is cut into two pieces: (i) transverse to its length, (ii) along its length?
(b) A magnetised needle in a uniform magnetic field experiences a torque but no net force. An iron nail near a bar magnet, however, experiences a force of attraction in addition to a torque. Why?
(c) Must every magnetic configuration have a north pole and a south pole? What about the field due to a toroid?
(d) Two identical looking iron bars A and B are given, one of which is definitely known to be magnetised. (We do not know which one.) How would one ascertain whether or not both are magnetised? If only one is magnetised, how does one ascertain which one? [Use nothing else but the bars A and B.]
Solution
(a) In either case, one gets two magnets, each with a north and south pole.
(b)
No force if the field is uniform. The iron nail experiences a non-uniform field due to the bar magnet. There is induced magnetic moment in the nail, therefore, it experiences both force and torque. The net force is attractive because the induced south pole (say) in the nail is closer to the north pole of magnet than induced north pole.
(c) Not necessarily. True only if the source of the field has a net non-zero magnetic moment. This is not so for a toroid or even for a straight infinite conductor.
(d) Try to bring different ends of the bars closer. A repulsive force in some situation establishes that both are magnetised. If it is always attractive, then one of them is not magnetised. In a bar magnet the intensity of the magnetic field is the strongest at the two ends (poles) and weakest at the central region. This fact may be used to determine whether A or B is the magnet. In this case, to see which
one of the two bars is a magnet, pick up one, (say, A) and lower one of its ends; first on one of the ends of the other (say, B), and then on the middle of B. If you notice that in the middle of B, A experiences no force, then B is magnetised. If you do not notice any change from the end to the middle of B, then A is magnetised.