In Chapter 1, we studied Gauss’s law for electrostatics. In Fig 5.3(c), we see that for a closed surface represented by i , the number of lines leaving the surface is equal to the number of lines entering it. This is consistent with the fact that no net charge is enclosed by the surface. However, in the same figure, for the closed surface ii , there is a net outward flux, since it does include a net (positive) charge.
The situation is radically different for magnetic fields which are continuous and form closed loops. Examine the Gaussian surfaces represented by i or ii in Fig 5.3(a) or Fig. 5.3(b). Both cases visually demonstrate that the number of magnetic field lines leaving the surface is balanced by the number of lines entering it. The net magnetic flux is zero for both the surfaces. This is true for any closed surface.

Karl Friedrich Gauss (1777 – 1855) He was a child prodigy and was gifted in mathematics, physics, engineering, astronomy and even land surveying. The properties of numbers fascinated him, and in his work he anticipated major mathematical development of later times. Along with Wilhelm Welser, he built the first electric telegraph in 1833. His mathematical theory of curved surface laid the foundation for the later work of Riemann.
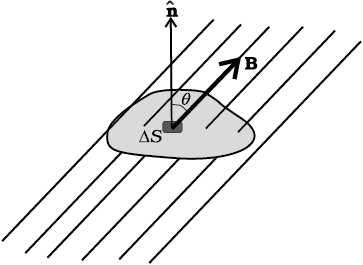
Figure 5.6
Consider a small vector area element ∆S of a closed surface S as in Fig. 5.6. The magnetic flux through ΔS is defined as ∆φB = B.∆S, where B is the field at ∆S. We divide S into many small area elements and calculate the individual flux through each. Then, the net flux φB is,
(5.9)
where ‘all’ stands for ‘all area elements ∆S′. Compare this with the Gauss’s law of electrostatics. The flux through a closed surface in that case is given by
where q is the electric charge enclosed by the surface.
The difference between the Gauss’s law of magnetism and that for electrostatics is a reflection of the fact that isolated magnetic poles (also called monopoles) are not known to exist. There are no sources or sinks of B; the simplest magnetic element is a dipole or a current loop. All magnetic phenomena can be explained in terms of an arrangement of dipoles and/or current loops.
Thus, Gauss’s law for magnetism is:
The net magnetic flux through any closed surface is zero.
Example 5.6 Many of the diagrams given in Fig. 5.7 show magnetic field lines (thick lines in the figure) wrongly. Point out what is wrong with them. Some of them may describe electrostatic field lines correctly. Point out which ones.

Figure 5.7
Solution
(a) Wrong. Magnetic field lines can never emanate from a point, as shown in figure. Over any closed surface, the net flux of B must always be zero, i.e., pictorially as many field lines should seem to enter the surface as the number of lines leaving it. The field lines shown, in fact, represent electric field of a long positively charged wire. The correct magnetic field lines are circling the straight conductor, as described in Chapter 4.
(b) Wrong. Magnetic field lines (like electric field lines) can never cross each other, because otherwise the direction of field at the point of intersection is ambiguous. There is further error in the figure. Magnetostatic field lines can never form closed loops around empty space. A closed loop of static magnetic field line must enclose a region across which a current is passing. By contrast, electrostatic field lines can never form closed loops, neither in empty space, nor when the loop encloses charges.
(c) Right. Magnetic lines are completely confined within a toroid. Nothing wrong here in field lines forming closed loops, since each loop encloses a region across which a current passes. Note, for clarity of figure, only a few field lines within the toroid have been shown. Actually, the entire region enclosed by the windings contains magnetic field.
(d) Wrong. Field lines due to a solenoid at its ends and outside cannot be so completely straight and confined; such a thing violates Ampere’s law. The lines should curve out at both ends, and meet eventually to form closed loops.
(e) Right. These are field lines outside and inside a bar magnet. Note carefully the direction of field lines inside. Not all field lines emanate out of a north pole (or converge into a south pole). Around both the N-pole, and the S-pole, the net flux of the field is zero.
(f) Wrong. These field lines cannot possibly represent a magnetic field. Look at the upper region. All the field lines seem to emanate out of the shaded plate. The net flux through a surface surrounding the shaded plate is not zero. This is impossible for a magnetic field. The given field lines, in fact, show the electrostatic field lines around a positively charged upper plate and a negatively charged lower plate. The difference between Fig. [5.7(e) and (f)] should be carefully grasped.
(g) Wrong. Magnetic field lines between two pole pieces cannot be precisely straight at the ends. Some fringing of lines is inevitable. Otherwise, Ampere’s law is violated. This is also true for electric field lines.
Example 5.7
(a) Magnetic field lines show the direction (at every point) along which a small magnetised needle aligns (at the point). Do the magnetic field lines also represent the lines of force on a moving charged particle at every point?
(b) Magnetic field lines can be entirely confined within the core of a toroid, but not within a straight solenoid. Why?
(c) If magnetic monopoles existed, how would the Gauss’s law of magnetism be modified?
(d) Does a bar magnet exert a torque on itself due to its own field? Does one element of a current-carrying wire exert a force on another element of the same wire?
(e) Magnetic field arises due to charges in motion. Can a system have magnetic moments even though its net charge is zero?
Solution
(a) No. The magnetic force is always normal to B (remember magnetic force = qv × B). It is misleading to call magnetic field lines as lines of force.
(b) If field lines were entirely confined between two ends of a straight solenoid, the flux through the cross-section at each end would be non-zero. But the flux of field B through any closed surface must always be zero. For a toroid, this difficulty is absent because it has no ‘ends’.
(c) Gauss’s law of magnetism states that the flux of B through any closed surface is always zero.
If monopoles existed, the right hand side would be equal to the monopole (magnetic charge) qmenclosed by S. [Analogous to Gauss’s law of electrostatics,where qm is the (monopole) magnetic charge enclosed by S.]
(d) No. There is no force or torque on an element due to the field produced by that element itself. But there is a force (or torque) on an element of the same wire. (For the special case of a straight wire, this force is zero.)
(e) Yes. The average of the charge in the system may be zero. Yet, the mean of the magnetic moments due to various current loops may not be zero. We will come across such examples in connection with paramagnetic material where atoms have net dipole moment through their net charge is zero.