Figure 7.12 shows a series LCR circuit connected to an ac source ε. As usual, we take the voltage of the source to be v = vm sin ωt.
If q is the charge on the capacitor and i the current, at time t, we have, from Kirchhoff’s loop rule:
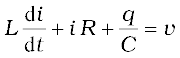 (7.20)
(7.20)
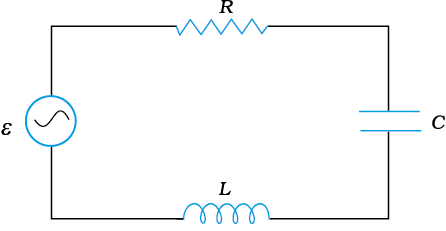
FIGURE 7.12 A series LCR circuit connected to an ac source.
We want to determine the instantaneous current i and its phase relationship to the applied alternating voltage v. We shall solve this problem by two methods. First, we use the technique of phasors and in the second method, we solve Eq. (7.20) analytically to obtain the time–dependence of i.
From the circuit shown in Fig. 7.12, we see that the resistor, inductor and capacitor are in series. Therefore, the ac current in each element is the same at any time, having the same amplitude and phase. Let it be
i = im sin(ωt+φ) (7.21)
where φ is the phase difference between the voltage across the source and the current in the circuit. On the basis of what we have learnt in the previous sections, we shall construct a phasor diagram for the present case.
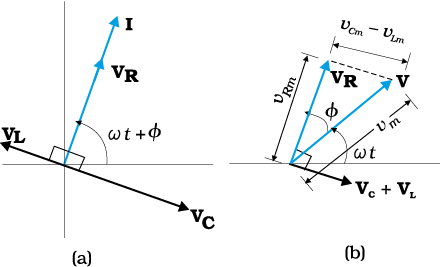
Figure 7.13 (a) Relation between the phasors VL, VR, VC, and I, (b) Relation between the phasors VL, VR, and (VL + VC) for the circuit in Fig. 7.11.
Let I be the phasor representing the current in the circuit as given by Eq. (7.21). Further, let VL, VR, VC, and V represent the voltage across the inductor, resistor, capacitor and the source, respectively. From previous section, we know that VR is parallel to I, VC is π/2 behind I and VL is π/2 ahead of I. VL, VR, VC and I are shown in Fig. 7.13(a) with apppropriate phase-relations.
The length of these phasors or the amplitude of VL, VR, VC are:
vRm = im R, vCm = im XC, vLm = im XL (7.22)
The voltage Equation (7.20) for the circuit can be written as
vL + vR + vC = v (7.23)
The phasor relation whose vertical component gives the above equation is
VL + VR + VC = V (7.24)
This relation is represented in Fig. 7.13(b). Since VC and VL are always along the same line and in opposite directions, they can be combined into a single phasor (VC + VL) which has a magnitude |vCm – vLm.| Since V is represented as the hypotenuse of a right-triangle whose sides are VR and (VC + VL), the pythagorean theorem gives:
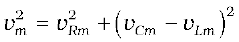
Substituting the values of vRm, vCm, and vLm from Eq. (7.22) into the above equation, we have
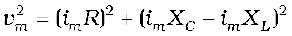
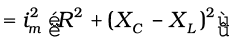
or, 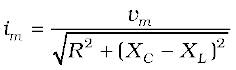 [7.25(a)]
[7.25(a)]
By analogy to the resistance in a circuit, we introduce the impedance Z in an ac circuit:
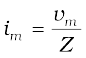 [7.25(b)]
[7.25(b)]
where 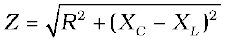 (7.26)
(7.26)
Since phasor I is always parallel to phasor VR, the phase angle φ is the angle between VR and V and can be determined from
Fig. 7.14:
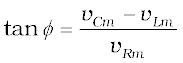
Using Eq. (7.22), we have
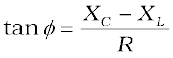 (7.27)
(7.27)
Equations (7.26) and (7.27) are graphically shown in Fig. (7.14). This is called Impedance diagram which is a right-triangle with Z as its hypotenuse.
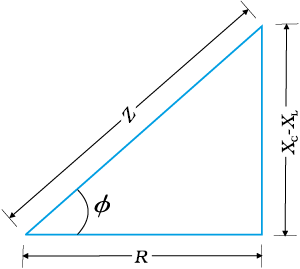
Figure 7.14 Impedance diagram.
Equation 7.25(a) gives the amplitude of the current and Eq. (7.27) gives the phase angle. With these, Eq. (7.21) is completely specified.
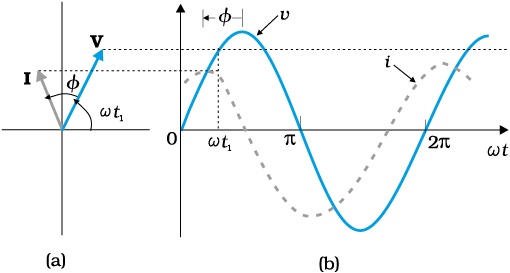
If XC > XL, φ is positive and the circuit is predominantly capacitive. Consequently, the current in the circuit leads the source voltage. If XC < XL, φ is negative and the circuit is predominantly inductive. Consequently, the current in the circuit lags the source voltage.
Figure 7.15 shows the phasor diagram and variation of v and i with ωt for the case XC > XL.
Thus, we have obtained the amplitude and phase of current for an LCR series circuit using the technique of phasors. But this method of analysing ac circuits suffers from certain disadvantages. First, the phasor diagram say nothing about the initial condition. One can take any arbitrary value of t (say, t1, as done throughout this chapter) and draw different phasors which show the relative angle between different phasors.
The solution so obtained is called the steady-state solution. This is not a general solution. Additionally, we do have a transient solution which exists even for v = 0. The general solution is the sum of the transient solution and the steady-state solution. After a sufficiently long time, the effects of the transient solution die out and the behaviour of the circuit is described by the steady-state solution.