2.6.1 Orbitals and Quantum Numbers

 A large number of orbitals are possible in an atom. Qualitatively these orbitals can be distinguished by their size, shape and orientation. An orbital of smaller size means there is more chance of finding the electron near the nucleus. Similarly shape and orientation mean that there is more probability of finding the electron along certain directions than along others. Atomic orbitals are precisely distinguished by what are known as quantum numbers. Each orbital is designated by three quantum numbers labelled as n, l and ml.

 The principal quantum number ‘n’ is a positive integer with value of n = 1,2,3....... The principal quantum number determines the size and to large extent the energy of the orbital. For hydrogen atom and hydrogen like species (He+, Li2+, .... etc.) energy and size of the orbital depends only on ‘n’.

The principal quantum number also identifies the shell. With the increase in the value of ‘n’, the number of allowed orbital increases and are given by ‘n2’ All the orbitals of a given value of ‘n’ constitute a single shell of atom and are represented by the following letters

n = 1 2 3 4 ............

Shell = K L M N ............

Size of an orbital increases with increase of principal quantum number ‘n’. In other words the electron will be located away from the nucleus. Since energy is required in shifting away the negatively charged electron from the positively charged nucleus, the energy of the orbital will increase with increase of n.

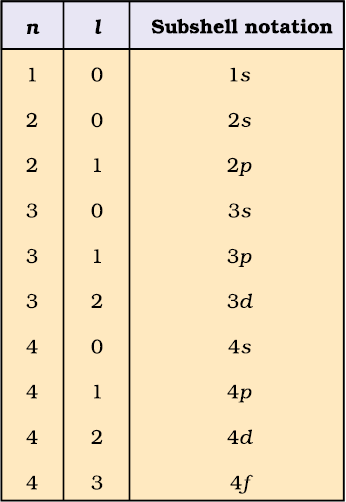
 Azimuthal quantum number. ‘l’ is also known as orbital angular momentum or subsidiary quantum number. It defines the three-dimensional shape of the orbital. For a given value of n, l can have n values ranging from 0 to n – 1, that is, for a given value of n, the possible value of l are : l = 0, 1, 2, .......... (n–1)

For example, when n = 1, value of l is only 0. For n = 2, the possible value of l can be 0 and 1. For n = 3, the possible l values are 0, 1 and 2.

Each shell consists of one or more sub-shells or sub-levels. The number of sub-shells in a principal shell is equal to the value of n. For example in the first shell (n = 1), there is only one sub-shell which corresponds to l = 0. There are two sub-shells (l = 0, 1) in the second shell (n = 2), three (l = 0, 1, 2) in third shell (n = 3) and so on. Each sub-shell is assigned an azimuthal quantum number (l). Sub-shells corresponding to different values of l are represented by the following symbols.

Value for l : 0 1 2 3 4 5 ............

notation for s p d f g h ............

sub-shell

Table 2.4 shows the permissible values of ‘l ’ for a given principal quantum number and the corresponding sub-shell notation.

  Magnetic orbital quantum number. ‘ml’ gives information about the spatial orientation of the orbital with respect to standard set of co-ordinate axis. For any sub-shell (defined by ‘l’ value) 2l+1 values of ml are possible and these values are given by :

ml = – l, – (l–1), – (l–2)... 0,1... (l–2), (l–1), l

Thus for l = 0, the only permitted value of ml = 0, [2(0)+1 = 1, one s orbital]. For l = 1, ml can be –1, 0 and +1 [2(1)+1 = 3, three p orbitals]. For l = 2, ml = –2, –1, 0, +1 and +2, [2(2)+1 = 5, five d orbitals]. It should be noted that the values of ml are derived from l and that the value of l are derived from n.

Table 2.4 Subshell Notations

 Each orbital in an atom, therefore, is defined by a set of values for n, l and ml. An orbital described by the quantum numbers
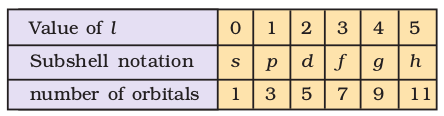
n = 2, l = 1, ml = 0 is an orbital in the p sub-shell of the second shell. The following chart gives the relation between the subshell and the number of orbitals associated with it.

 Electron spin ‘s’ : The three quantum numbers labelling an atomic orbital can be used equally well to define its energy, shape and orientation. But all these quantum numbers are not enough to explain the line spectra observed in the case of multi-electron atoms, that is, some of the lines actually occur in doublets (two lines closely spaced), triplets (three lines, closely spaced) etc. This suggests the presence of a few more energy levels than predicted by the three quantum numbers.

In 1925, George Uhlenbeck and Samuel Goudsmit proposed the presence of the fourth quantum number known as the electron spin quantum number (ms). An electron spins around its own axis, much in a similar way as earth spins around its own axis while revolving around the sun. In other words, an electron has, besides charge and mass, intrinsic spin angular quantum number. Spin angular momentum of the electron — a vector quantity, can have two orientations relative to the chosen axis. These two orientations are distinguished by the spin quantum numbers ms which can take the values of +½ or –½. These are called the two spin states of the electron and are normally represented by two arrows, ↑ (spin up) and ↓ (spin down). Two electrons that have different ms values (one +½ and the other –½) are said to have opposite spins. An orbital cannot hold more than two electrons and these two electrons should have opposite spins.

To sum up, the four quantum numbers provide the following information :

i) n defines the shell, determines the size of the orbital and also to a large extent the energy of the orbital.

ii) There are n subshells in the nth shell. l identifies the subshell and determines the shape of the orbital (see section 2.6.2). There are (2l+1) orbitals of each type in a subshell, that is, one s orbital (l = 0), three p orbitals (l = 1) and five d orbitals (l = 2) per subshell. To some extent l also determines the energy of the orbital in a multi-electron atom.

iii) ml designates the orientation of the orbital. For a given value of l, ml has (2l+1) values, the same as the number of orbitals per subshell. It means that the number of orbitals is equal to the number of ways in which they are oriented.

iv) ms refers to orientation of the spin of the electron.