A cylinder of \(500~\text{g}\) and radius \(10~\text{cm}\) has moment of inertia (about its natural axis):
1. \(2.5\times 10^{-3}~\text{kg-m}^2\)
2. \(2\times 10^{-3}~\text{kg-m}^2\)
3. \(5\times 10^{-3}~\text{kg-m}^2\)
4. \(3.5\times 10^{-3}~\text{kg-m}^2\)

Two rings of the same radius and mass are placed such that their centers are at a common point and their planes are perpendicular to each other. The moment of inertia of the system about an axis passing through the center and perpendicular to the plane of one of the rings is (mass of the ring and radius = r)

1.  $\frac{1}{2}{\mathrm{mr}}^2$

2.  ${\mathrm{mr}}^2$

3.  $\frac{3}{2}{\mathrm{mr}}^2$

4.  $2{\mathrm{mr}}^2$

In a rectangle ABCD (BC = 2AB). The moment of inertia along which axis will be minimum?
               
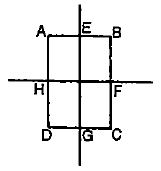
1. BC
2. BD
3. HF
4. EG

A wheel comprises of a ring of radius R and mass M and three spokes of mass m each. The moment of inertia of the wheel about its axis is

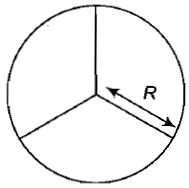
1.  \(\left(M   +   \frac{m}{4}\right) R^{2} \)

2.  \(\left(M   +   m\right) R^{2} \)

3.  \(\left(M   +   3 m\right) R^{2} \)

4.  \(\left(\frac{M   +   m}{2}\right) R^{2}\)

The angular velocity of a body changes from $\frac{1}{25}$ rev./sec to 1 rev./sec. without applying any torque. The ratio of its radius of gyration in two situations is :

1.  5: 1

2.  1: 5

3.  1: 25

4.  25: 1

A solid cylinder and a solid sphere, both having the same mass and radius, are released from a rough inclined plane. Both roll without slipping. Then,

1.  the force of friction that acts on the two is the same

2.  the force of friction is greater in the case of a sphere than in a cylinder

3.  the force of friction is greater in the case of a cylinder than in a sphere

4.  the force of friction will depend on the nature of the surface of the body that is moving and that of the inclined surface and is independent of the shape and size of the moving body

A homogeneous disc of mass 2 kg and radius 15 cm is rotating about its axis (which is fixed) with an angular velocity of 4 rad/sec. The linear momentum Of the disc is 

1.  1.2 kg m/sec 

2.  1.0 kg m/sec 

3.  0.6 kg m/sec 

4.  None of these

A rigid body rotates about a fixed axis with a variable angular velocity equal to \(\alpha -\beta t\), at the time \(t\), where \(\alpha , \beta\) are constants. The angle through which it rotates before it stops is:

For the uniform T shaped structure, with mass \(3~ \text M\), the moment of inertia about an axis normal to the plane and passing through O would be

            

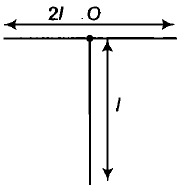
1. \({ 2 \over 3} \text {MI}^2\)
2. \(\text {MI}^2\)
3. \({ MI^2 \over 3}\)
4. None of these