| (a) | obeys Maxwell’s distribution. |
| (b) | have the same value for all molecules. |
| (c) | equals the translational kinetic energy for each molecule. |
| (d) | is \(\frac{2}{3}\text{rd}\) the translational kinetic energy for each molecule. |
| 1. | (a), (b) | 2. | (a), (d) |
| 3. | (c), (d) | 4. | (a), (c) |
Which of the following diagrams (figure) depicts ideal gas behaviour?
| 1. | (a), (c) | 2. | (a), (d) |
| 3. | (c), (d) | 4. | (a), (b) |
When an ideal gas is compressed adiabatically, its temperature rises: the molecules on an average have more kinetic energy than before. The kinetic energy increases:
| 1. | because of collisions with moving parts of the wall only. |
| 2. | because of collisions with the entire wall. |
| 3. | because the molecules get accelerated in their motion inside the volume. |
| 4. | because of the redistribution of energy amongst the molecules. |
A cubic vessel (with faces horizontal \(+\) vertical) contains an ideal gas at NTP. The vessel is being carried by a rocket which is moving at a speed of \(500~\text{ms}^{-1}\) in the vertical direction. The pressure of the gas inside the vessel as observed by us on the ground:
| 1. | remains the same because \(500~\text{ms}^{-1}\) is very much smaller than \(v_\text{rms}\) of the gas. |
| 2. | remains the same because the motion of the vessel as a whole does not affect the relative motion of the gas molecules and the walls. |
| 3. | will increase by a factor equal to \(\left(\dfrac{v_\text{rms}^2+(500)^2}{v_\text{rms}^2}\right) \) where \(v_\text{rms}^2\) was the original mean square velocity of the gas. |
| 4. | will be different on the top wall and bottom wall of the vessel. |
\(1\) mole of an ideal gas is contained in a cubical volume V, ABCDEFGH at \(300\) K (figure). One face of the cube (EFGH) is made up of a material which totally absorbs any gas molecule incident on it. At any given time:
| 1. | the pressure on EFGH would be zero. |
| 2. | the pressure on all the faces will be equal. |
| 3. | the pressure on EFGH would be double the pressure on ABCD. |
| 4. | the pressure on EFGH would be half that on ABCD. |
Boyle's law is applicable for an:
| 1. | adiabatic process | 2. | isothermal process |
| 3. | isobaric process | 4. | isochoric process |
A cylinder containing an ideal gas is in a vertical position and has a piston of mass \(M\) that is able to move up or down without friction (figure). If the temperature is increased,

| 1. | both \(P\) and \(V\) of the gas will change. |
| 2. | only \(P\) will increase according to Charles' law. |
| 3. | \(V\) will change but not \(P.\) |
| 4. | \(P\) will change but not \(V.\) |
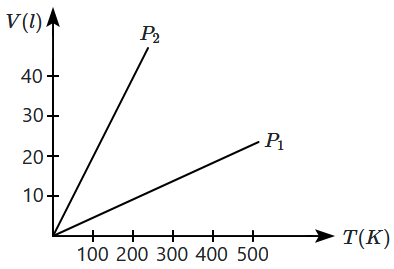
The volume versus temperature graphs for a given mass of an ideal gas are shown in the figure at two different values of constant pressure. What can be inferred about relation between \(\mathrm{P_1}\) and \(\mathrm{P_2}\)?
1. \(\mathrm{P_1}>\mathrm{P_2} \)
2. \(\mathrm{P_1}=\mathrm{P_2} \)
3. \(\mathrm{P_1}<\mathrm{P_2} \)
4. data is insufficient
(considering all gases to be ideal)
| 1. | same as the pressure initially. |
| 2. | \(2\) times the pressure initially. |
| 3. | \(10\) times the pressure initially. |
| 4. | \(20\) times the pressure initially. |
An inflated rubber balloon contains one mole of an ideal gas, has a pressure \(P,\) volume \(V\) and temperature \(T.\) If the temperature rises to \(1.1T,\) and the volume is increased to \(1.05V,\) the final pressure will be:
| 1. | \(1.1P\) |
| 2. | \(P\) |
| 3. | less than \(P\) |
| 4. | between \(P\) and \(1.1P\) |