On average, a human heart is found to beat 75 times in a minute. Its frequency and period respectively are:
1. 2.25 Hz and 0.8 sec
2. 1.35 Hz and 0.9 sec
3. 1.25 Hz and 0.8 sec
4. 1.25 kHz and 0.8 sec
(\(\omega\) is any positive constant)
| (a) | \((\sin\omega t+ \cos \omega t)\) |
| (b) | \((\sin\omega t+ \cos 2\omega t+ \sin4\omega t)\) |
| (c) | \(e^{-\omega t}\) |
| (d) | \(\mathrm{log(\omega t)}\) |
| (e) | \(\sin^{2}\omega t\) |
Choose the correct option from the given ones:
| 1. | (a) only |
| 2. | (a), (b), and (d) only |
| 3. | (a), (b), and (e) only |
| 4. | All of these |
| (a) | \(\sin\omega t+ \cos\omega t\) |
| (b) | \(\sin\omega t+ \cos2\omega t+ \sin4\omega t\) |
2. \(\dfrac{2 \pi}{\omega} \text{ for both}\)
3. \(\dfrac{2 \pi}{3 \omega} \text{ for both}\)
4. \(\dfrac{3 \pi}{\omega} \text{ and } \dfrac{2 \pi}{\omega}\)
Given the following simple harmonic motion.
(A) \(\sin\omega t - \cos\omega t\)
(B) \(\sin^{2}\omega t\)
The time period motions respectively are:
1. \(\dfrac{2 \pi}{\omega} \text{ and } \dfrac{\pi}{\omega}\)
2. \(\dfrac{2 \pi}{\omega} \text{ and }\dfrac{\pi}{2 \omega}\)
3. \(\dfrac{2 \pi}{\omega} \text{ and }\dfrac{4 \pi}{\omega}\)
4. \(\dfrac{\pi}{\omega} \text{ and } \dfrac{3 \pi}{\omega}\)
The figure given below depicts two circular motions. The radius of the circle, the period of revolution, the initial position, and the sense of revolution are indicated in the figures. Equations of the \(x\)-projection of the radius vector of the rotating particle \(\mathrm P\) in each case are, respectively:
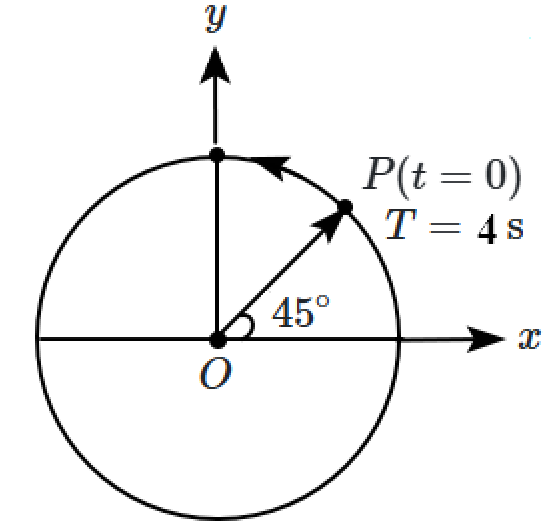
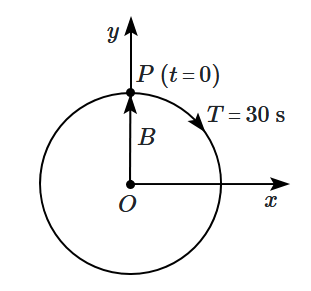
| 1. | \(\small{x}({t})={A} \cos \left(\dfrac{2 \pi}{4} {t}+\dfrac{\pi}{4}\right)\text{ and }{x}({t})={B} \cos \left(\dfrac{\pi}{15} {t}-\dfrac{\pi}{2}\right)\) |
| 2. | \(\small{x}({t})={A} \cos \left(\dfrac{2 \pi}{4} {t}+\dfrac{\pi}{4}\right)\text{ and }{x}({t})={B} \sin \left(\dfrac{\pi}{15} {t}-\dfrac{\pi}{2}\right)\) |
| 3. | \(\small{x}({t})={A} \cos \left(\dfrac{2 \pi}{4} {t}+\dfrac{\pi}{4}\right)\text{ and }{x}({t})={B} \cos \left(\dfrac{\pi}{15} {t}-\dfrac{\pi}{4}\right)\) |
| 4. | \(\small{x}({t})={A} \sin \left(\dfrac{2 \pi}{4} {t}+\dfrac{\pi}{4}\right)\text{ and }{x}({t})={B} \cos \left(\dfrac{\pi}{15} {t}-\dfrac{\pi}{2}\right)\) |
A body oscillates with SHM according to the equation (in SI units) \(x = 5\cos\left[2\pi t +\frac{\pi}{4}\right]\). At \(t = 1.5\) s, the displacement and speed of the body respectively are:
1. \(3.535~\text{m}~\text{and}~24~\text{m/s}\)
2. \(-3.535~\text{m}~\text{and}~24~\text{m/s}\)
3. \(-3.535~\text{m}~\text{and}~22~\text{m/s}\)
4. \(3.535~\text{m}~\text{and}~22~\text{m/s}\)
Two identical springs of spring constant \(k\) are attached to a block of mass \(m\) and to fixed supports as shown in the figure. When the mass is displaced from its equilibrium position on either side, it executes a simple harmonic motion. The period of oscillations is:

1. \(2 \pi \sqrt{\dfrac{{m}}{4{k}}}\)
2. \(2 \pi \sqrt{\dfrac{2{m}}{{k}}}\)
3. \(2 \pi \sqrt{\dfrac{{m}}{2{k}}}\)
4. \(2 \pi \sqrt{\dfrac{{m}}{{k}}}\)
A block whose mass is \(1\) kg is fastened to a spring. The spring has a spring constant of \(50~\text{Nm}^{-1}\). The block is pulled to a distance \(x = 10\) cm from its equilibrium position at \(x = 0\) on a frictionless surface from rest at \(t=0.\) The kinetic energy of the block when it is \(5\) cm away from the mean position is:
1. \(1.9~\text{J}\)
2. \(0.29~\text{J}\)
3. \(0.19~\text{J}\)
4. \(2.9~\text{J}\)
What is the length of a simple pendulum, which ticks seconds?
1. \(0.5~\text{m}\)
2. \(1~\text{m}\)
3. \(5~\text{m}\)
4. \(2~\text{m}\)
A 5 kg collar is attached to a spring of spring constant 500 N/m. It slides without friction over a horizontal rod. The collar is displaced from its equilibrium position by 10.0 cm and released. The period of oscillation of the collar is:
1.
2.
3.
4.






