Q. No.In an astronomical telescope in normal adjustment, a straight line of length \(L\) is drawn on the inside part of the objective lens. The eye-piece forms a real image of this line. The length of this image is \(l.\) The magnification of the telescope is:
1. \(\frac{L}{l}+1\)
2. \(\frac{L}{l}-1\)
3. \(\frac{L+1}{l-1}\)
4. \(\frac{L}{l}\)
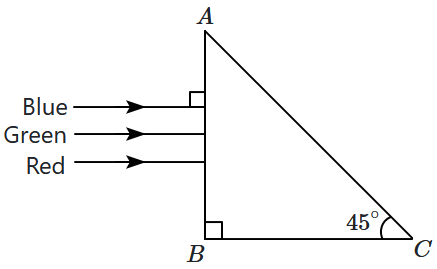
The prism will:
| 1. | separate the blue colour part from the red and green colour. |
| 2. | separate all the three colours from one another. |
| 3. | not separate the three colours at all. |
| 4. | separate the red colour part from the green and blue colours. |
Two identical thin plano-convex glass lenses (refractive index = \(1.5\)) each having radius of curvature of \(20\) cm are placed with their convex surfaces in contact at the centre. The intervening space is filled with oil of a refractive index of \(1.7\). The focal length of the combination is:
1. \(-20\) cm
2. \(-25\) cm
3. \(-50\) cm
4. \(50\) cm
| 1. | \(180^\circ-3A\) | 2. | \(180^\circ-2A\) |
| 3. | \(90^\circ-A\) | 4. | \(180^\circ+2A\) |
If the focal length of the objective lens is increased then the magnifying power of:
| 1. | microscope will increase but that of the telescope decrease. |
| 2. | microscope and telescope both will increase. |
| 3. | microscope and telescope both will decrease. |
| 4. | microscope will decrease but that of the telescope will increase. |
The angle of a prism is \(A\). One of its refracting surfaces is silvered. Light rays falling at an angle of incidence \(2{A}\) on the first surface return back through the same path after suffering reflection at the silvered surface. The refractive index \(\mu,\) of the prism, is:
1. \(2\text{sin}A\)
2. \(2\text{cos}A\)
3. \(\frac{1}{2}\text{cos}A\)
4. \(\text{tan}A\)
| 1. | \(\dfrac{R}{2(\mu_1-\mu_2)}\) | 2. | \(\dfrac{R}{(\mu_1-\mu_2)}\) |
| 3. | \(\dfrac{2R}{(\mu_2-\mu_1)}\) | 4. | \(\dfrac{R}{2(\mu_1+\mu_2)}\) |
For a normal eye, the cornea of the eye provides a converging power of \(40~\text{D}\) and the least converging power of the eye lens behind the cornea is \(20~\text{D}\). Using this information, the distance between the retina and the cornea-eye lens can be estimated to be:
1. \(2.5~\text{cm}\)
2. \(1.67~\text{cm}\)
3. \(1.5~\text{cm}\)
4. \(5~\text{cm}\)
| 1. | the scattering of light. |
| 2. | the polarisation of light. |
| 3. | the colour of the sun. |
| 4. | the colour of the sky. |
1. \(45^\circ\)
2. \(30^\circ\)
3. \(55^\circ\)
4. \(50^\circ\)
© 2024 GoodEd Technologies Pvt. Ltd.