We can charge a metal sphere positively without touching it by:
1. Conduction
2. Induction
3. Friction
4. Both (1) and (2)
If \(10^9\) electrons move out of a body to another body every second, how much time approximately is required to get a total charge of \(1\) C on the other body?
1. \(200\) years
2. \(100\) years
3. \(150\) years
4. \(250\) years
The amount of positive and negative charges in a cup of water (\(250\) g) are respectively:
| 1. | \(1.6 \times10^9\) C, \(1.4 \times10^9\) C |
| 2. | \(1.4 \times10^9\) C, \(1.6 \times10^9\) C |
| 3. | \(1.34 \times10^7\) C, \(1.34 \times10^7\) C |
| 4. | \(1.6 \times10^8\) C, \(1.6 \times10^7\) C |
The ratio of the magnitude of electric force to the magnitude of gravitational force for an electron and a proton will be:
(\(m_p=1.67\times10^{-27}~\text{kg}\), \(m_e=9.11\times10^{-31}~\text{kg}\))
1. \(2.4\times10^{39}\)
2. \(2.6\times10^{36}\)
3. \(1.4\times10^{36}\)
4. \(1.6\times10^{39}\)
A charged metallic sphere \(A\) is suspended by a nylon thread. Another identical charged metallic sphere \(B\) held by an insulating handle is brought close to \(A\) such that the distance between their centres is \(10\) cm, as shown in Fig.(a). The resulting repulsion of \(A\) is noted. Then spheres \(A\) and \(B\) are touched by identical uncharged spheres \(C\) and \(D\) respectively, as shown in Fig.(b). \(C\) and \(D\) are then removed and \(B\) is brought closer to \(A\) to a distance of \(5.0\) cm between their centres, as shown in Fig. (c). What is the expected repulsion on \(A\) on the basis of Coulomb’s law?
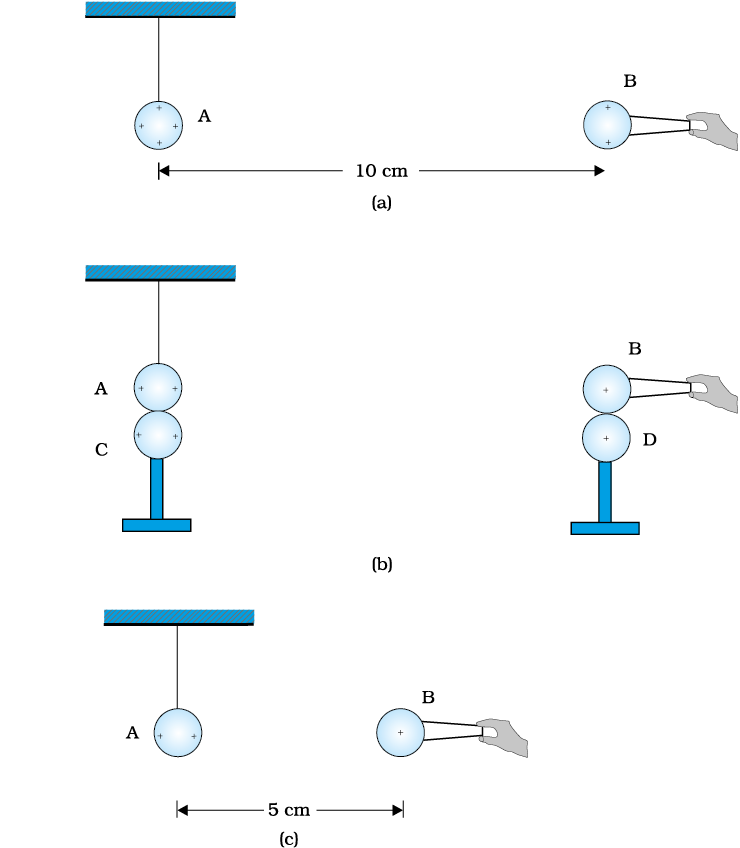
| 1. | Electrostatic force on \(A\) due to \(B\) remains unaltered. |
| 2. | Electrostatic force on \(A\) due to \(B\) becomes double. |
| 3. | Electrostatic force on \(A\) due to \(B\) becomes half. |
| 4. | Can't say. |
Consider three charges \(q_1,~q_2,~q_3\) each equal to \(q\) at the vertices of an equilateral triangle of side \(l.\) What is the force on a charge \(Q\) (with the same sign as \(q\)) placed at the centroid of the triangle, as shown in the figure?
1. \(\dfrac{3}{4\pi \epsilon _{0}} \dfrac{Qq}{l^2}\)
2. \(\dfrac{9}{4\pi \epsilon _{0}} \dfrac{Qq}{l^2}\)
3. zero
4. \(\dfrac{6}{4\pi \epsilon _{0}} \dfrac{Qq}{l^2}\)
Consider the charges \(q,~q,\) and \(-q\) placed at the vertices of an equilateral triangle, as shown in the figure. Then the sum of the forces on the three charges is:
1. \(\frac{1}{4\pi \epsilon _{0}}\frac{q^{2}}{l^{2}}\)
2. zero
3. \(\frac{2}{4\pi \epsilon _{0}}\frac{q^{2}}{l^{2}}\)
4. \(\frac{3}{4\pi \epsilon _{0}}\frac{q^{2}}{l^{2}}\)
An electron falls through a distance of \(1.5~\text{cm}\) in a uniform electric field of magnitude \(2\times10^4~\text{N/C}\) [figure (a)]. The direction of the field is reversed keeping its magnitude unchanged and a proton falls through the same distance [figure (b)]. If \(t_e\) and \(t_p\) are the time of fall for electron and proton respectively, then:
1. \(t_e=t_p\)
2. \(t_e>t_p\)
3. \(t_e<t_p\)
4. none of these
Two-point charges and , of magnitude and , respectively, are placed 0.1 m apart. The electric field at point A (as shown in the figure) is:
Two charges \(\pm10~\mu\text{C}\) are placed \(5.0\) mm apart. The electric field at a point \(P\) on the axis of the dipole \(15\) cm away from its centre \(O\) on the side of the positive charge, as shown in the figure is:
| 1. | \(2.7\times10^5~\text{NC}^{-1}\) |
2. | \(4.13\times10^6~\text{NC}^{-1}\) |
| 3. | \(3.86\times10^6~\text{NC}^{-1}\) | 4. | \(1.33\times10^5~\text{NC}^{-1}\) |










