A car is moving along a straight line, say \(OP\) in the figure. It moves from \(O\) to \(P\) in \(18\) s and returns from \(P\) to \(Q\) in \(6.0\) s. The average velocity and average speed of the car in going from \(O\) to \(P\) and back to \(Q\) respectively are:
1. \(10\) m/s & \(10\) m/s
2. \(20\) m/s & \(30\) m/s
3. \(20\) m/s & \(20\) m/s
4. \(10\) m/s & \(20\) m/s
The position of an object moving along \(x\)-axis is given by \(x=a+bt^2\), where \(a=8.5\) m, \(b=2.5 \text{ ms}^{-2}\) and \(t\) is measured in seconds. Its average velocity between \(t=2.0\) s and \(t=4.0\) s is:
1. \(10~\text{m/s}\)
2. \(15~\text{m/s}\)
3. \(20~\text{m/s}\)
4. \(25~\text{m/s}\)
Which of the following does not represent the equation of motion for constant acceleration?
| 1. | \(v=v_0+at\) | 2. | \(v^2=v_0^2+2a(x-x_0)\) |
| 3. | \(x = x_0v_0+\dfrac{1}{2}at^2\) | 4. | \(x = x_0+v_0t+\dfrac{1}{2}at^2\) |
(Take \(g=10\) m/s2)
| 1. | \(30\) m | 2. | \(25\) m |
| 3. | \(45\) m | 4. | \(20\) m |
A ball is thrown vertically upwards with a velocity of \(20\) m/s from the top of a multistorey building. The height of the point from where the ball is thrown is \(25.0\) m from the ground. How long will it be before the ball hits the ground?
(Take \(g=10\) ms–2.)
1. \(3\) s
2. \(2\) s
3. \(5\) s
4. \(20\) s
When brakes are applied to a moving vehicle, the distance it travels before stopping is called stopping distance. It is an important factor for road safety and depends on the initial velocity \({v_0}\) and the braking capacity, or deceleration, \(-a\) that is caused by the braking. Expression for stopping distance of a vehicle in terms of \({v_0}\) and \(a\) is:
| 1. | \(\dfrac{{v_o}^2}{2a}\) | 2. | \(\dfrac{{v_o}}{2a}\) |
| 3. | \(\dfrac{{v_o}^2}{a}\) | 4. | \(\dfrac{2a}{{v_o}^2}\) |
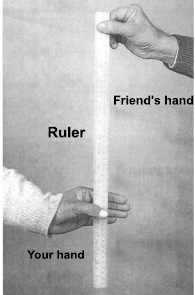
You can measure your reaction time by a simple experiment. Take a ruler and ask your friend to drop it vertically through the gap between your thumb and forefinger (figure shown below). After you catch it if the distance d travelled by the ruler is \(21.0\) cm, your reaction time is:
| 1. | \(0.2\) s | 2. | \(0.4\) s |
| 3. | \(0\) | 4. | \(0.1\) s |
Galileo’s law of odd numbers: The distances traversed, during equal intervals of time, by a body falling from rest, stand to one another in the ratio:
| 1. | as the odd numbers beginning with unity. |
| 2. | as the even numbers beginning with unity. |
| 3. | as the square of odd numbers beginning with unity. |
| 4. | as the square of even numbers beginning with unity. |
A train is moving in south with a speed of 90 . The velocity of ground with respect to the train is:
1. 0
2. -25
3. 25
4. -40
Two parallel rail tracks run north-south. Train A moves north with a speed of 54 , and train B moves south with a speed of 90 . The magnitude of the velocity of B with respect to A is:
1. 40
2. 0
3. 25
4. 15







